Die Corona-Krise bietet die seltene Gelegenheit, gleichsam in Echtzeit zu verfolgen, wie eine Forschungswissenschaft funktioniert. Was wir dank der Berichterstattung in den Medien über Virologie und Epidemiologie erfahren, ist aber nicht auf diese Disziplinen beschränkt, sondern lässt sich auf andere Disziplinen wie die Unterrichtsforschung übertragen.
Ausgehend von der Unterscheidung der Forschungsparadigmen Experiment, Statistik und Fallstudie bin ich im zweiten Teil meines Beitrags auf die experimentelle Unterrichtsforschung eingegangen. Der Vorzug des Experiments liegt in seinem eingreifenden Charakter, d.h. in der Möglichkeit, den Forschungsgegenstand durch Variation seiner Bedingungen und Kontrolle von Störfaktoren systematisch zu untersuchen.
Enge ethische Grenzen für das Experiment
Aus praktischen und ethischen Gründen sind dem Experiment in der pädagogischen Forschung aber Grenzen gesetzt. So ist es kaum möglich, Schulklassen allein zu Untersuchungszwecken und für die Dauer einer experimentellen Intervention willkürlich zusammenzusetzen oder das Verhalten von Lehrpersonen so weit zu standardisieren, dass es von persönlichen Einflüssen frei ist. Ebenso wenig lassen sich Studien unter Bedingungen durchführen, die sich negativ auf die Schülerinnen und Schüler auswirken könnten. Wo sich experimentelle Eingriffe verbieten, ist man daher auf die Untersuchung natürlicherweise variierender Bedingungen angewiesen. Dabei dient die Statistik als wichtiges Hilfsmittel der Datenanalyse. Davon soll im dritten Teil meines Beitrags die Rede sein.
Organisierte und unorganisierte Komplexität
In einem Aufsatz mit dem Titel Science and Complexity unterschied der Mathematiker Warren Weaver (1948) drei Arten von Problemen, nämlich einfache Probleme, Probleme unorganisierter Komplexität und Probleme organisierter Komplexität. Unerwähnt blieben die komplizierten Probleme, weshalb Weaver die experimentelle Methode lediglich für die Analyse von einfachen Problemen für zuständig hielt. Das ändert aber nichts an der Aussage im zweiten Teil meines Beitrags, wonach auch komplizierte Probleme experimentell untersucht werden können, sofern sie sich in einfache zerlegen lassen.
In der Tat befasst sich die Statistik mit Phänomenen, die zwar von gleicher Art sind, aber in keiner Beziehung zueinander stehen. Das trifft beispielsweise auf die Gesamtheit aller Schülerinnen und Schüler im Alter von 14 Jahren in der Stadt Bern zu, auf alle Einwohnerinnen und Einwohner der Schweiz, die täglich den öffentlichen Verkehr benutzen, oder auf sämtliche Roulettespiele, die an einem Stichtag im Casino Baden stattgefunden haben.
Weavers zweite und dritte Art von Problemen unterscheiden sich dadurch, dass wir es im Fall von unorganisierter Komplexität mit Massenphänomenen zu tun haben, die keine innere Ordnung aufweisen, während im Fall von organisierter Komplexität Phänomene vorliegen, wie wir sie im zweiten Teil des Beitrags erwähnt haben: Wetterlagen, Kerzenflammen und Unterricht. Weaver hielt Probleme organisierter Komplexität aufgrund ihrer Vielschichtigkeit für wissenschaftlich unzugänglich. Ob er damit auch heute noch Recht hat, mag man bezweifeln, jedoch trifft zweifellos zu, dass für die Analyse der verbleibenden Probleme unorganisierter Komplexität die Statistik zuständig ist.
In der Tat befasst sich die Statistik mit Phänomenen, die zwar von gleicher Art sind, aber in keiner Beziehung zueinander stehen. Das trifft beispielsweise auf die Gesamtheit aller Schülerinnen und Schüler im Alter von 14 Jahren in der Stadt Bern zu, auf alle Einwohnerinnen und Einwohner der Schweiz, die täglich den öffentlichen Verkehr benutzen, oder auf sämtliche Roulettespiele, die an einem Stichtag im Casino Baden stattgefunden haben.
Vom Nutzen der Statistik
Wie beim Experiment macht es zunächst den Eindruck, als sei die Statistik für die Untersuchung von pädagogischen Phänomenen wie dem Unterricht nicht geeignet. Denn im Falle einer Schulklasse haben wir es zweifellos nicht mit unorganisierter, sondern mit organisierter Komplexität zu tun. Aber wie das Experiment genutzt werden kann, indem wir Komplexität behandeln, als ob es sich um Kompliziertheit handelt, können wir die Statistik nutzen, indem wir organisierte Komplexität behandeln, als hätten wir es mit unorganisierter Komplexität zu tun. Genau diese Unterstellung liegt den meisten Studien der empirischen Unterrichtsforschung zugrunde.
Statistische Verfahren sind nicht gegenstandsneutrale Methoden, die nach Belieben eingesetzt werden können, sondern beruhen auf mathematischen Modellen, denen Annahmen über die Beschaffenheit des Forschungsgegenstandes zugrunde liegen. Kommt ein statistisches Verfahren zum Einsatz, muss daher gewährleistet sein, dass der Gegenstand den Annahmen des mathematischen Modells entspricht. Zu diesen Annahmen gehört, wie bereits angedeutet, dass die Ereignisse, die in eine statistische Analyse eingehen, unabhängig voneinander sind, also keine innere Ordnung aufweisen. Während das einzelne Ereignis – zum Beispiel der Wurf einer Münze – vielfach determiniert sein kann, ist die Summe der Ereignisse – zum Beispiel eine Serie von hundert Würfen mit derselben Münze – ohne inneren Zusammenhang. Es handelt sich m.a.W. um Zufallsereignisse.
Das heisst auch, dass der Einzelfall statistisch nicht von Belang ist. Was interessiert, sind Zusammenhänge zwischen Variablen
Das heisst auch, dass der Einzelfall statistisch nicht von Belang ist. Was interessiert, sind Zusammenhänge zwischen Variablen und Unterschiede in der Verteilung von Merkmalen, die idealerweise repräsentativ für die Verhältnisse in der Grundgesamtheit sind, über die man sich informieren will. Während die deskriptive Statistik die Daten lediglich beschreibt, hat die schliessende Statistik (Inferenzstatistik) zum Ziel, die Wahrscheinlichkeit abzuschätzen, dass ein Ergebnis zufällig zustande gekommen ist, d.h. nur für die untersuchte Stichprobe gilt, in einer anderen aber möglicherweise anders ausfallen würde. Abgesichert werden solche Schlüsse von der Stichprobe auf die Grundgesamtheit u.a. mit Hilfe von Signifikanztests.
Vom Signifikanztest zur Effektstärke
Signifikanztests verfahren nach einer Logik, die intuitiv nicht leicht nachvollziehbar ist. Denn im Falle eines empirisch aufgedeckten Unterschieds in der Verteilung eines Merkmals wird davon ausgegangen, dass der Unterschied faktisch nicht existiert (sog. Nullhypothese). Danach wird überprüft, wie wahrscheinlich es ist, dass die Nullhypothese zutrifft. Stellt sich nun heraus, dass diese Wahrscheinlichkeit gering ist, wird die eigentlich interessierende Hypothese, dass der Unterschied besteht, als zutreffend akzeptiert. Die Irrtumswahrscheinlichkeit entspricht dem Signifikanzniveau, für das man sich vor Durchführung des Signifikanztests entschieden hat. Dieses liegt nach einer weit verbreiteten Konvention bei α = .05 (eher geringe Wahrscheinlichkeit eines Irrtums), α = .01 (geringe Wahrscheinlichkeit eines Irrtums) oder α = 001 (sehr geringe Wahrscheinlichkeit eines Irrtums).
Ein statistisch signifikantes Ergebnis bedeutet demnach, dass für einen in einer Untersuchungsgruppe (Stichprobe) aufgedeckten Unterschied (zum Beispiel zwischen Jungen und Mädchen) unter der Annahme, dass der Unterschied real nicht existiert, wenig Plausibilität besteht, weshalb gefolgert wird, dass das Ergebnis mit einer gewissen Irrtumswahrscheinlichkeit zutrifft. Wie man sieht, beruht die Argumentation auf einer indirekten Beweisführung, insofern nicht getestet wird, was interessiert (es gibt einen Unterschied), sondern was nicht interessiert (es gibt keinen Unterschied), wobei genau genommen nicht Ergebnisse getestet werden, sondern die Wahrscheinlichkeit, bei der Annahme eines Ergebnisses einem Irrtum zu erliegen. Da das Verfahren rein formal ist, lässt sich aus der Tatsache, dass ein empirisches Ergebnis einen Signifikanztest erfolgreich bestanden hat, nicht schliessen, dass es auch – in theoretischer oder praktischer Hinsicht – relevant ist, und zwar egal welches Signifikanzniveau gewählt wurde.
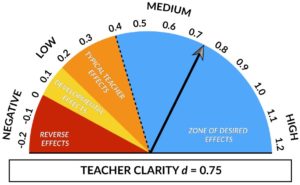
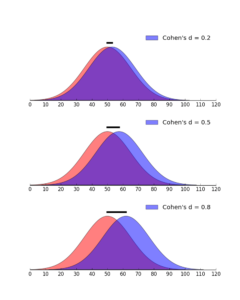
Aussagekräftiger hinsichtlich der Bedeutsamkeit von Ergebnissen der Unterrichtsforschung sind im Vergleich mit einem Signifikanztest Masszahlen für deren Effektstärke. Die Effektstärke gibt an, wie gross ein statistisch signifikanter Unterschied zwischen zwei Untersuchungsgruppen ist. Das vieldiskutierte Buch von John Hattie (2009) über die Wirksamkeit verschiedener Einflussfaktoren auf die Lernleistung von Schülerinnen und Schülern beruht ganz auf der Aufbereitung und dem Vergleich solcher Effektstärken. Dabei postuliert Hattie eine Effektstärke von d = .40 als Grenze, ab der ein Ergebnis als pädagogisch relevant beurteilt werden kann. Nach einem Vorschlag von Jacob Cohen gelten Effektstärken von d = .20 als klein, von d = .50 als mittel und von d = .80 als gross. Dementsprechend ist die Glaubwürdigkeit der Lehrperson, die bei Hatte mit einer Effektstärke von d = .90 ausgewiesen wird, von grossem Einfluss auf das Schülerlernen. Von etwas geringerer Relevanz ist die Klarheit der Lehrperson (d = .75), während die Lehrer-Schüler-Beziehung (d = .52) und die Lernunterstützung durch die Eltern (d = .50) von mittlerer und ein schülerzentrierter Unterricht (d = .36), Hausaufgaben (d = .29) sowie die Lehrerpersönlichkeit (d = .23) von geringer Bedeutung für den Lernerfolg der Schülerinnen und Schüler sind.
Hatties Analyse, die inzwischen eine Liste von 277 Wirkfaktoren umfasst, ist typisch für das Vorgehen der Unterrichtsforschung, die ihre Methoden nur einsetzen kann, wenn sie die Komplexität des Unterrichts drastisch reduziert.
Hatties Analyse, die inzwischen eine Liste von 277 Wirkfaktoren umfasst, ist typisch für das Vorgehen der Unterrichtsforschung, die ihre Methoden nur einsetzen kann, wenn sie die Komplexität des Unterrichts drastisch reduziert. Sie tut es, indem sie einzelne Bedingungsfaktoren herauslöst und auf ihren Einfluss auf das Schülerlernen untersucht. Unbeantwortet bleiben dabei die Fragen nach allfälligen Beziehungen oder Interaktionen zwischen den Einflussfaktoren sowie der Veränderung ihrer Wirksamkeit und ihres Zusammenspiels über die Zeit hinweg. Die Komplexität, die bei der Datenerhebung aus methodischen Gründen reduziert wird, lässt sich bei der Datenanalyse nicht zurückgewinnen.
Der ökologische Fehlschluss
Da statistische Werte nicht für Einzelfälle, sondern für Verteilungen stehen und diese mittels Kennzahlen wie Mittelwerten oder Streuungsmassen charakterisieren, liegen statistische Aussagen auf einer Ebene, deren Bezug zur Wirklichkeit oft als zweifelhaft erscheint. Was «im Durchschnitt» gilt, kann sich im Einzelfall als falsch erweisen, oder es fehlt ihm eine reale Entsprechung. Schülerinnen und Schüler existieren zwar im Plural, aber nicht als statistischer Mittelwert. Der Schluss von der aggregierten Ebene der Massendaten auf den Einzelfall gilt daher als fehlerhaft und wird ökologischer Fehlschluss genannt.
Wenn sich zum Beispiel in einer Studie, die an 60 Schulklassen durchgeführt wurde, herausstellt, dass Unterrichtsstörungen vorwiegend von Schülern, aber kaum von Schülerinnen ausgehen, dann handelt es sich dabei um ein Ergebnis, das – unter Auswertung sämtlicher Daten auf der globalen Ebene sämtlicher Schülerinnen und Schüler – einen wesentlichen Unterschied zwischen den Geschlechtern markiert. Daraus lässt sich aber nicht schliessen, dass in jeder einzelnen der untersuchten 60 Klassen vorwiegend die Schüler den Unterricht stören. Genauso wenig lässt sich aufgrund des Ergebnisses schliessen, dass es immer nur die Schüler sind, von denen Unterrichtsstörungen ausgehen. Obwohl es statistisch gesehen korrekt ist zu sagen, Schüler würden den Unterricht im Allgemeinen eher stören als Schülerinnen, kann es sich im Einzelnen genau umgekehrt verhalten.
Fiktionale Wirklichkeit?
Man kann dies kritisch beurteilen und die pädagogisch-psychologische Forschung, die sich statistischer Methoden bedient, der Verfehlung des Individuums bezichtigen. So hat Klaus Holzkamp (1985) der modernen Psychologie vorgeworfen, Wissenschaftlichkeit auf Kosten der Subjektivität zu betreiben. Mittels statistischer Analysen werde eine «artifizielle Unperson» (S. 30) kreiert, ein «statistisches Gespenst» (ebd.), das von den realen historischen und gesellschaftlichen Bedingungen, unter denen Menschen in ihrem Alltag leben, losgetrennt sei. Trotz dieser scharfen Kritik glaubte Holzkamp jedoch nicht, dass mit der Verbannung der Statistik aus der Psychologie viel gewonnen wäre. In der Tat ist schwer zu sehen, wie in einer modernen Forschungswissenschaft auf das Instrumentarium der Statistik verzichtet werden könnte.
Die Frage ist daher nicht, ob wir mit Hilfe der Statistik ein falsches Bild von der Unterrichtswirklichkeit gewinnen. Auch im Falle der experimentellen Erforschung des Unterrichts wäre dies eine falsch gestellte Frage. Weder im einen noch im anderen Fall vermögen wir durch die blosse Anwendung einer Methode Klarheit über die Qualität unserer Erkenntnisse zu erlangen. Erst wenn die Ergebnisse einer Studie einem kritischen Diskurs in der Gemeinschaft der Forscherinnen und Forscher unterzogen werden und dem Diskurs standhalten, besteht Anlass zur Vermutung, dass wir einen Zipfel der Wahrheit erwischt haben.
Qualitative Forschung als Alternative?
Die bisherige Diskussion zeigt, dass weder das Experiment noch die Statistik in der Lage sind, die Komplexität der Unterrichtswirklichkeit ohne Abstriche einzufangen. In beiden Fällen muss das Untersuchungsobjekt vereinfacht werden, um einer wissenschaftlichen Analyse zugänglich zu sein. Dies führt nicht selten zum Vorwurf, die empirische Unterrichtsforschung würde ihren Gegenstand verfehlen. Als Alternative werden qualitative Studien empfohlen, die besser in der Lage seien, die komplexe Wirklichkeit von Schule und Unterricht einzufangen. Im vierten Teil meines Beitrags werde ich mich mit dieser Auffassung auseinandersetzen und die Fallstudie als Forschungsparadigma der Unterrichtsforschung unter die Lupe nehmen.
Literaturverzeichnis
Holzkamp, Klaus (1985). Selbsterfahrung und wissenschaftliche Objektivität: Unaufhebbarer Widerspruch? In: Karl-Heinz Braun & Klaus Holzkamp (Hrsg.): Subjektivität als Problem psychologischer Methodik (S. 17-37). Frankfurt a.M.: Campus.
Hattie, John A. C. (2009).Visible Learning. A Synthesis of Over 800 Meta-Analyses Relating to Achievement. London: Routledge.
Weaver, Warren (1948). Science and Complexity. American Scientist (36), 536-544.
