
Das sind 0,5 bzw. 0,6 Promille, würde der Mathematiklehrer mit der Mathematik der Primarschule im Gepäck sagen – oder würde der Polizist dem alkoholisierten Autofahrer in der Schweiz mitteilen und ihn auffordern, sein Auto stehenzulassen. Im europäischen Coronaspiel ist etwas anderes gemeint. Es geht um die Überschreitung einer Zahl 50 von wöchentlichen bzw. im Schweizer Sonderweg einer Zahl 60 von zweiwöchentlichen angeblichen Neuinfektionen mit SARS-CoV-2, bezogen auf die Einwohnerzahl des betreffenden Landes oder Gebietes.
Ein primitiver Algorithmus
Der Algorithmus für den Corona-Alarm ist primitiv: Zähle für die Bezugszeitperiode von 1 bzw. 2 Wochen alle gemeldeten positiven Fälle (“Neuinfektionen”) unter den Testungen. Wie viele Tests insgesamt durchgeführt wurden, bleibt unberücksichtigt, um das freie Spiel nicht zu gefährden.
Diese Aktionen sind also von Regierungsseite weitgehend frei steuerbar durch planvollen Testumfang.
Dividiere die Positivenzahl durch die Einwohnerzahl der betreffenden Region und multipliziere diesen Quotienten mit 100.000. Ist das Resultat größer als 50 bzw. 60, wird Alarm gegeben und die Region zum Risikogebiet erklärt. Und es folgen Maßnahmen gemäß dem politischen Stufenplan. Diese Aktionen sind also von Regierungsseite weitgehend frei steuerbar durch planvollen Testumfang.

Der bayrische Ministerpräsident Markus Söder nutzte jüngst die Gunst der Stunde der erfolgreichen Überschreitung der 0,5-Promillegrenze im Coronaspiel und zog die Zügel für München enger und fester: Fortan dürfen keine sechs Freunde sich mehr auf einem privaten Fest treffen können und schon Fünfe im Freien auf dem Viktualienmarkt oder Marienplatz nicht ohne Maske. Das schadet zwar der Wirtschaft des Freistaats Bayern nicht allgemein, aber mancher Gastwirtschaft schon: Das Traditionslokal Donisl am Marienplatz schließt zum Jahresende.
PCR-Test zeigt keine Erkrankung
 Die Modellierer unter den Mathematiklehrern sind hier gefordert. Oder eher gerade die nicht, weil das gute alte Sachrechnen hier gefragt ist? Um welche Sache geht es? Um den PCR-Test, der zwei kurze Sequenzstücke identifizieren soll, die im RNA-Genom von SARS-CoV-2 in der Regel zu finden sind. Er kann keine intakten Viren anzeigen, sondern er reagiert bereits auf Virenschrott, der sogar von anderen Coronaviren stammen kann, wie der letzte Ringversuch des deutschen RKI aufzeigt. Erst recht zeigt er keine Erkrankung an. Infizierung ist nicht gleich Erkrankung, sonst müssten alle Menschen krank sein, da wir alle mit einer Handvoll Viren infiziert sind. Das prominenteste ist das Epstein-Barr-Virus, das etwa 95 % der Menschen hierzulande in sich tragen. Die Sache selbst sieht also gar nicht gut aus, weil auch im Corona-Falle die asymptomatischen Fälle eine Größenordnung häufiger sind als die Erkrankungsfälle.
Die Modellierer unter den Mathematiklehrern sind hier gefordert. Oder eher gerade die nicht, weil das gute alte Sachrechnen hier gefragt ist? Um welche Sache geht es? Um den PCR-Test, der zwei kurze Sequenzstücke identifizieren soll, die im RNA-Genom von SARS-CoV-2 in der Regel zu finden sind. Er kann keine intakten Viren anzeigen, sondern er reagiert bereits auf Virenschrott, der sogar von anderen Coronaviren stammen kann, wie der letzte Ringversuch des deutschen RKI aufzeigt. Erst recht zeigt er keine Erkrankung an. Infizierung ist nicht gleich Erkrankung, sonst müssten alle Menschen krank sein, da wir alle mit einer Handvoll Viren infiziert sind. Das prominenteste ist das Epstein-Barr-Virus, das etwa 95 % der Menschen hierzulande in sich tragen. Die Sache selbst sieht also gar nicht gut aus, weil auch im Corona-Falle die asymptomatischen Fälle eine Größenordnung häufiger sind als die Erkrankungsfälle.
Das macht doch nichts, das merkt doch keiner (https://www.youtube.com/watch?v=gk32xp9Gnqs). Und es ist ja auch nur ein Spiel um ‘… und du bist raus’. Welchen Zusammenhang hat die Anzahl der in einem Zeitraum positiv Getesteten mit der Bevölkerungsgröße? Absolut keinen, außer der trivialen Tatsache, dass es in einem Gebiet nicht mehr Positivtestungen geben kann als Einwohner – es sei denn, man testet jeden Positiven fast täglich neu. Aber es suggeriert, dass man doch angeblich mit relativen Größen rechnete, wo keine sind. Das merkt doch keiner.
Der verdiente Lohn für das horrende Testen war dann tatsächlich der verliehene Status des Risikogebietes.
Die Zahl der Positiven, aufgesammelt in freier Wildbahn (z.B. an Bahnhöfen oder Flughäfen), muss zwingend ins Verhältnis zur Stichprobengröße gesetzt werden, also zur Anzahl aller durchgeführten Testungen in der jeweiligen Zeitperiode. Die Einwohnerzahl ist egal, solange sie größer als die Stichprobe ist. In Luxemburg hat man es beispielsweise am 6. August geschafft, im Verlaufe des Jahres bis dahin schon mehr Menschen getestet zu haben, als es Einwohner hat. Luxemburg war im Juli Testweltmeister:
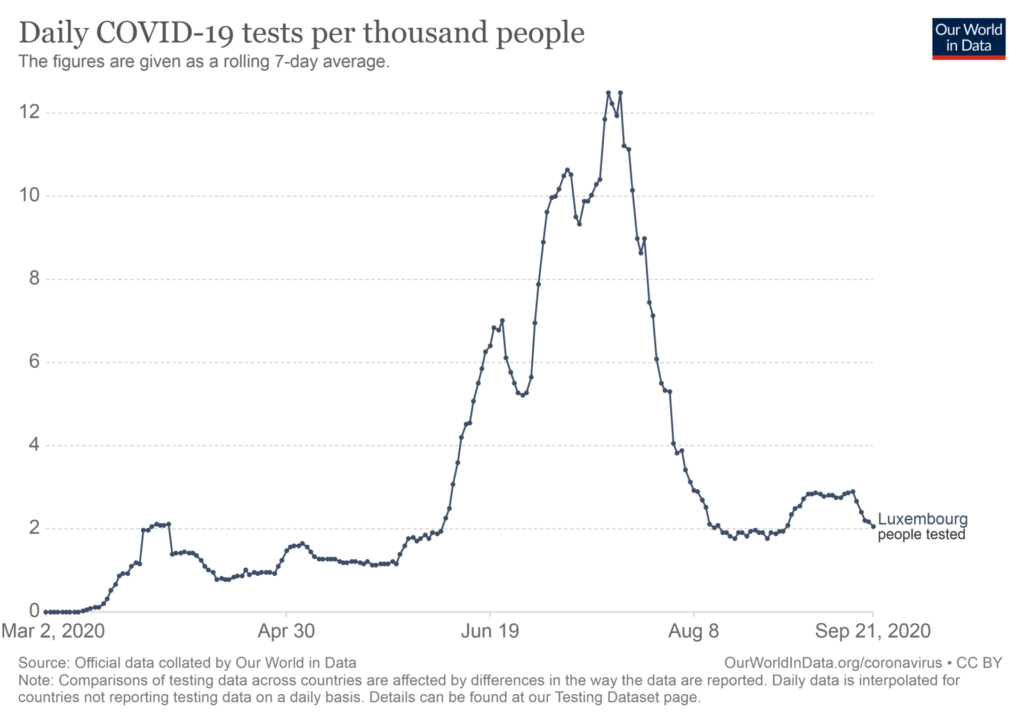
Pro Tausend gab es dort im laufenden Wochenmittel im Juli offensichtlich mehr als sieben mal acht, also 56 Tests. Schon unter der Prämisse, dass der Anteil der Positivergebnisse an den Testungen gemittelt mindestens 0,9 % war, wäre im ganzen Juli der Risikostatus erreicht gewesen, denn 56 mal hundert mal 0,9 % ist größer als 50. Der verdiente Lohn für das horrende Testen war dann tatsächlich der verliehene Status des Risikogebietes.
Es war nur ein Spiel, denn Gefahr war nicht im Verzug, als das Testen hochgefahren wurde: Vom 25. Mai bis 11. Juli war niemand in Luxemburg mit CoViD-19 verstorben. Dann vom 12. Juli bis 18. August gab es die letzten 11 CoViD-19-Toten (https://ourworldindata.org/covid-deaths?country=~LUX), wohl als Opfer der leichten Sommergrippe, die in unseren Breiten mindestens eine Größenordnung geringer ausfällt als die Wintergrippe. Warum hat man ausgerechnet inmitten der langen CoViD-todesfreien Periode die Testungen irrsinnig hochgefahren, um sie dann inmitten des Ansteigens der sommerlichen Todesrate jäh wieder zurückzufahren? Das kann der Mathematiker nicht beantworten und auch der gesunde Menschenverstand setzt hier aus.
Das ist im Kopfe gerechnet (- das sieht der Lehrplan 21 allerdings nicht vor) 100 mal 208 geteilt durch eine Million, also genau gleich 2,08 %. Die Rechnung in den Rechner einzutippen, dauert länger und ist fehleranfälliger.
Und die Schweiz?
Warum geht die Schweiz einen Sonderweg? Schauen wir virtuell von der Schweiz nach Deutschland und rechnen. Man muss davon ausgehen, dass in naher Zukunft die vorhandenen Laborkapazitäten in Deutschland etwas besser ausgeschöpft werden und wöchentlich genau 1,2 Millionen PCR-Tests abgewickelt werden. Bei welchem Anteil positiver Tests wird die Zwei-Wochen-Schwelle von 60 gerissen? Das ist eine schöne Rechenaufgabe für das Ende der Primarschule. Die gesuchte Zahl 60 soll sich ergeben aus dem Produkt der zweiwöchigen Neuinfektionenzahl, also 2,4 Millionen mal der unbekannten Positvenrate x, dividiert durch die Zahl 832 (aktuelle Bevölkerungsgröße Deutschlands geteilt durch 100.000). Damit ist x gleich 60 mal 832 durch 2,4 Millionen. Das ist im Kopfe gerechnet (- das sieht der Lehrplan 21 allerdings nicht vor) 100 mal 208 geteilt durch eine Million, also genau gleich 2,08 %. Die Rechnung in den Rechner einzutippen, dauert länger und ist fehleranfälliger.

Was bedeutet das Ergebnis im Kontext? Im Vergleich hat die Schweiz laut BAG derzeit eine Positivenrate von 3-5 % unter der Woche (also Wochenende ausgenommen). Aha! Mit Positivenrate 2,1 % ist Deutschland dann schon Risikoland und die Grenze zur Schweiz wird dann mehr oder weniger dichtgemacht. Diese Rate hatte es gerade noch in der 19. Kalenderwoche überschritten, wodurch das Ende der Epidemie zum Aprilende gekennzeichnet ist. Seit Ende Juni ist die Positivenrate in Deutschland stets unter 1 %. Aus Schweizer Sicht muss man sich fragen, warum gerade in Deutschland so ein Bohei um Corona gemacht wird: Da ist doch ohnehin seit Mai fast nichts an wirklichen Infektionen, Hospitalisierungen und Todesfällen mit CoViD-19 mehr los. Wir haben allerdings nicht lauter Berge, sondern einen Lauterbach, der laut genug kassandriert, um öffentliches Gehör bei der Regierung zu finden.
Aber darum geht es ja nicht. Es ist ja nur ein Reality-Spiel mit Gewinnern und Verlierern. “Die Entgrenzung der alltäglichen Erfahrung beruht wesentlich darauf, dass der Forschungsgegenstand durch Variation seiner Bedingungen systematisch untersucht wird” (Walter Herzog). Variieren wir also die Bedingungen: Wenn es der deutschen Regierung beliebt, kann es ja flugs die Testungszahl auf gut 400 000 pro Woche wieder herunterfahren, wie sie damals in der 19. Kalenderwoche bestand. Dann wird die Schweizer Alarmschwelle erst mit 6,3 % Anteil positiver Testungen überschritten. Es gab dieses Jahr als Wochenmaximum in Deutschland gerade mal die Rate 9,03 %. Um sogar unter dieser Schwelle zu bleiben, dürfte man in einer Woche höchstens gut 230 000 Personen testen.
Für die Schweiz selbst, die ja eine gewisse Tradition der Grenzabschottung kennt, ist aber die Zwei-Wochen-Schwelle 60 auch intern sehr wichtig. Man kann dann ausrechnen, bei wieviel Testungen und welcher Positivenrate es für welche Kantönli dann eng wird. Das muss zwingend in dem Spiel passieren, damit die Zügel mancherorts wieder straffer gezogen werden können. Und man den Bürgern sagen kann: Ihr wart dort zu leichtsinnig.
Lässt der Lehrplan 21 noch dieses entgrenzte Rechnen und Interpretieren der Ergebnisse zu? Wenn nicht, wäre für die Schweizer Schule “Denken als Lernziel” eine schöne Perspektive.






