
Frau Stern, Sie sind auf einem Bauernhof in Hessen aufgewachsen, heute sind Sie Professorin an der ETH Zürich. Wäre ein solcher Werdegang weiterhin möglich?
Möglich schon, aber weniger wahrscheinlich. Ich bin in einer Zeit der Bildungsexpansion gross geworden. Der Anteil der Gymnasiasten nahm jedes Jahr zu. Da war es kein Problem, dass leistungsfähige Kinder aus nichtakademischen Elternhäusern ans Gymnasium kamen.
Ist das heute anders?
Es ist Konsens, dass die Gymnasialquoten in Deutschland und in der Schweiz
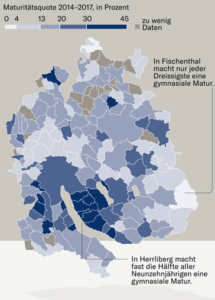
nicht erhöht werden sollen. Das Boot ist voll. Doch für Akademikereltern ist es schwer zu akzeptieren, dass ihre Kinder nicht ans Gymnasium gehen sollen. Also unternehmen sie sehr viel, damit es trotzdem klappt. Das kann zulasten von jenen Kindern gehen, die die Intelligenz eigentlich mitbringen, deren Eltern aber nicht den Hintergrund haben, um sie zu unterstützen.
Sie haben die Mathematikaufgaben der Zürcher Gymiprüfung einmal als willkürlich und zu anspruchsvoll kritisiert. Eine Aufgabe fürs Langgymnasium vom vergangenen Frühling lautet: 125 × 6,408. Ist das derart schwierig, dass man dafür einen teuren Vorbereitungskurs braucht?*
Hier ist geschicktes Rechnen gefragt. Dazu muss man verstanden haben, wie man Zahlen zerlegt. Viele der Textaufgaben, die ich gesehen habe, sind sehr verschlungen. Intelligente Kinder, die guten Mathematikunterricht hatten und so etwas einmal geübt haben, können das lösen. Aber wenn man Mathematikunterricht hatte, der nicht darauf angelegt war, einen vernetzten Zahlenraum aufzubauen, ist man benachteiligt.
Und so gibt es immer wieder Kinder, die die Aufnahmeprüfung nicht schaffen, obwohl sie das Zeug fürs Gymnasium hätten. Und es gibt Kinder, die so getrimmt werden, dass sie durchkommen, obwohl sie nicht übermässig intelligent sind.
Die Prüfungskommission stellt sich auf den Standpunkt, dass die Aufnahmeprüfung auf Primarschulstoff beruhe. Man könne sie auch ohne spezielles Training bestehen.
Theoretisch ist das so – wenn alle Kinder gute Lerngelegenheiten hätten. Aber die Kollegen wissen auch, dass es im Mathematikunterricht grosse Unterschiede gibt. Einer der Verantwortlichen hat mir vor einem Jahr gesagt: «Wir müssen sicherstellen, dass die Kinder solche Aufgaben einmal gesehen haben in der Schule.» Und so gibt es immer wieder Kinder, die die Aufnahmeprüfung nicht schaffen, obwohl sie das Zeug fürs Gymnasium hätten. Und es gibt Kinder, die so getrimmt werden, dass sie durchkommen, obwohl sie nicht übermässig intelligent sind.
Akademikereltern sehen, wenn in der Schule wenig anregende Aufgaben durchgenommen werden – und sorgen rechtzeitig dafür, dass das Kind zusätzliches Training erhält.
Dann liegt das Problem eher am Mathematikunterricht und weniger an der Prüfung?
Genau. Man kann sich seinen Primarlehrer nicht aussuchen. Akademikereltern sehen, wenn in der Schule wenig anregende Aufgaben durchgenommen werden – und sorgen rechtzeitig dafür, dass das Kind zusätzliches Training erhält. Nichtakademikereltern können das vielleicht nicht erkennen. Sie sehen nur die guten Noten und sind dann erstaunt, wenn ihr Kind durch die Prüfung fällt.
Dieses Jahr haben es in Zürich 4661 Schülerinnen und Schüler versucht, 8 Prozent mehr als 2020. Bestanden haben 48,7 Prozent – 3 Prozent weniger als im Jahr davor. Mehr Prüflinge, mehr Durchgefallene: Das spricht für die Gymiprüfung.
Die Prüfung muss schwer sein. Aber schwierige Aufgaben allein sind kein Indikator für einen guten Test. Wenn die Hälfte der Kinder einen Test besteht und die andere Hälfte nicht, hängt viel vom Zufall ab, ob man die Hürde gerade so überspringt oder nicht. Die Gymiprüfung sollte die intellektuelle Leistungsfähigkeit von Kandidaten vorhersagen, die alle die gleichen Lerngelegenheiten hatten.

Und wenn eine Schülerin besonders fleissig ist und vor allem deswegen durchkommt?
Mit Fleiss allein funktioniert das nur bis zu einem gewissen Alter. Je anspruchsvoller der Schulstoff wird, desto weniger kann man später kompensieren. Das sehen wir auch in den ersten Semestern an der ETH. Für die Prüfungen muss man gute geistige Voraussetzungen mitbringen. Wir müssen dafür sorgen, dass beim Zugang zum Gymnasium Intelligenz und Begabung zählen und nicht die soziale Herkunft.
Ein bekanntes Problem. Haben Sie eine Lösung dafür?
Ein guter Ansatz wäre: keine kommerziellen Kurse mehr – dafür bekommen alle Kinder mit guten Leistungen in der Primarschule die Gelegenheit, mit dafür ausgebildeten Lehrpersonen für die Gymiprüfung zu lernen. Dafür sollte man Geld in die Hand nehmen.
Und bei Zweifelsfällen, wenn die Lehrerin ein Kind nicht für geeignet hält, die Eltern hingegen schon oder umgekehrt: was dann?
Dann sollte man einen Intelligenztest machen. Das wäre eine Entscheidungshilfe.
Was bedeutet Intelligenz?
Geistige Flexibilität, schlussfolgerndes Denken, sich auf ein Ziel konzentrieren können. Irrelevante Informationen ausblenden, relevante aktivieren.
Es gibt auch intelligente Jugendliche, die Lust auf eine Lehre haben.
Solange sie das freiwillig machen, gerne. Aber ist es richtig, wenn kluge Köpfe Gymnasium, Matura und Studium gar nicht erst in Erwägung ziehen? Und wenn sich stattdessen andere durch Mittelschule und Uni schleppen und am Ende in einem Job landen, für den sie nicht geeignet sind? Die Schweiz kann sich den Luxus der tiefen Maturandenquote nur leisten, weil sie fehlende Akademiker im Bedarfsfall aus dem Ausland holen kann.
Wie viele Schüler sind im Gymnasium, die nicht dahin gehören?
Eine konservative Schätzung lautet: 30 Prozent.

Und an den Universitäten? An der ETH Zürich gibt es Brückenkurse für Studienanfänger in Mathematik und Programmieren und vielleicht bald in Chemie und Physik.
Das ist etwas anderes. Die Kurse sollen Defizite aus dem Gymnasium beheben, die auf einen schlechten Unterricht zurückzuführen sind, nicht auf mangelnde Intelligenz. Lehrermangel in Mathematik und Physik ist ein grosses Problem. Die Leute haben Alternativen. Viele Absolventen unserer Lehrerausbildung sagen mir im Abschlussgespräch: «Vielleicht unterrichte ich später mal, aber zuerst gehe ich in die Industrie.» Die Schulen müssen häufig Behelfslösungen finden mit Leuten, die noch nicht einmal einen Abschluss haben.
Was wäre zu tun, damit die besten Köpfe trotzdem Gymnasiallehrer würden?
Es kann sehr befriedigend sein, ein Fach weiterzugeben, das man mag. Forschung ist wichtig, aber Lehrer leisten einen genauso wichtigen Beitrag in der Gesellschaft. Das versuchen wir an der ETH zu vermitteln.

Was macht guten Unterricht aus in diesen Fächern?
Es geht darum, Konzepte so zu erläutern, dass sie verstanden werden. Also nicht einfach mit Formeln wie «Kraft = Masse × Beschleunigung» operieren, sondern ausgiebig besprechen, wie sich der Kraftbegriff in der Physik vom Kraftbegriff im Alltag unterscheidet. Oder dass jede Kraft eine Gegenkraft hat – eine abstrakte Vorstellung, die man der Klasse trotzdem näherbringen sollte, anstatt einfach zu sagen: «Das ist nun mal so.» Sonst verlieren intelligente Schüler das Interesse. Vor allem junge Frauen wollen verstehen und wenden sich dann anderen Fächern zu.
Das heisst, man sollte mit anschaulichen Beispielen arbeiten – wie bei der Frage, warum ein schweres Schiff aus Stahl schwimmt?
Das ist Primarschulstoff, am Gymnasium muss man abstrakte Konzepte vermitteln, die sehr erklärungsmächtig sind, aber keine Eigenschaften unserer wahrnehmbaren Welt haben. Gold hat die Farbe Gelb, aber das Goldatom hat keine Farbe. Minus mal minus ist plus. Das ist nicht intuitiv, aber Maturanden sollten verstanden haben, dass es eine innermathematische Logik gibt, die keine Alternative zulässt.
Das ist Primarschulstoff, am Gymnasium muss man abstrakte Konzepte vermitteln, die sehr erklärungsmächtig sind, aber keine Eigenschaften unserer wahrnehmbaren Welt haben.
Logik klingt gut. Aber wie berechnet man die Steigung einer linearen Funktion schon wieder?
Die Steigung des Graphen einer linearen Funktion ist der Quotient aus der Differenz der Koordinaten auf der y-Achse und jener der Koordinaten auf der x-Achse – für zwei beliebige Punkte auf dem Graphen. Klingt kompliziert. Aber das Entscheidende ist: Es geht um die Rate der Veränderung. Wenn man dieses Konzept verstanden hat, kann man es auf Stückpreise, Geschwindigkeit, Beschleunigung oder alles Mögliche anwenden.
Aber ein Text aus Wörtern und Sätzen hat schon Vorteile, weil er leichter zu verstehen ist als Formeln und mathematische oder physikalische Gesetze.
Das kommt auf den Text an. Lesen Sie mal einen Text zur Relativitätstheorie.
Touché. Aber auch da geht es um Physik!
Mathematik und Physik sind schwierig – auch weil die Inhalte in diesen Fächern stark aufeinander aufbauen. In Geschichte etwa kann man sich auf die Neuzeit konzentrieren, ohne alle anderen Epochen im Detail zu kennen. Man kann schlecht in Englisch sein und sich im Alltag trotzdem einigermassen verständigen. Aber wenn man in Mathematik und Physik bestimmte Konzepte nicht verstanden hat, hat man eigentlich gar nichts verstanden.
Die Schweiz braucht Fachkräfte. Wird es mit den zahlreichen Initiativen für guten Unterricht in Mathematik, Informatik, Naturwissenschaft und Technik (Mint) eines Tages gelingen, diesen Mangel zu entschärfen?
Das ist ein Motiv, es ist aber längst nicht das einzige. Schule soll vor allem helfen, die Welt zu verstehen. Aber die ETH hat natürlich nichts dagegen, wenn ihre Studenten bereit sind fürs Studium. Auch deshalb investieren wir in die Lehrerbildung. Wir möchten nicht, dass Maturanden bestimmte Optionen von vornherein ausschliessen, weil sie falsche Vorstellungen davon haben. Wir haben aber auch den Anspruch, dass Leute, die nicht Naturwissenschaften und Mathematik studieren, eine Idee davon haben, wie ein iPhone funktioniert und was alles passiert, bis der Strom aus der Steckdose kommt. Oder was exponentielles Wachstum ist. Das sollte man wissen, gerade in einer Pandemie, um Entwicklungen der Fallzahlen einordnen zu können.
Sollte man mit diesen Grundlagen schon in der Primarschule ansetzen?

Unbedingt. Eine Langzeitstudie unseres Lernzentrums an der ETH hat gezeigt, dass Achtjährige physikalische Fragen deutlich besser verstehen als Zwölfjährige, wenn sie altersgerechten naturwissenschaftlichen Unterricht bereits gehabt haben.
Darf man von einer Primarlehrerin erwarten, dass sie ihren Schülern neben Schreiben, Rechnen, Englisch, Französisch, Natur, Mensch, Gesellschaft auch Physik beibringt?
Man muss. Man kann sich auf wenige Themen beschränken wie Schwimmen und Sinken. Oder dass Schall ein Medium braucht, um sich auszubreiten. Dafür gibt es gute Unterrichtsmaterialien, die man allerdings einüben muss in der Aus- oder der Weiterbildung. Das geht nicht von allein im Unterricht.
Ist es sinnvoll, dass Primar- und Sekundarlehrer an den PH und Gymnasiallehrer weiterhin vor allem an Universitäten ausgebildet werden?
Diese riesige Diskrepanz ist ein Problem. Überspitzt formuliert könnte man sagen: Gymnasiallehrer haben sehr viel Fachwissen, lernen aber relativ wenig über Pädagogik. Und an den PH ist es genau umgekehrt. Das führt zu Berührungsängsten und manchmal auch zu einer Arroganz bei Gymnasiallehrern, die sagen: «Volksschullehrer können ja nix.» Dagegen kämpfen wir an.
Wie?
Eine meiner Mitarbeiterinnen macht gerade ein Seminar, wo Lehrerstudenten Sekundar- und Primarschulen besuchen und dort auch unterrichten müssen. Auch um zu sehen, was die Kinder bereits können und was die Kollegen dort mit ihnen machen.
Solange wir Defizite haben in Mathematik und Naturwissenschaften, sollte man nicht noch mehr Fächer ins Gymnasium packen.
Ein Ansatz für die Zukunft?
Ja, Gymnasiallehrer sollten vermehrt über die eigene Schulstufe hinausblicken.
Psychologie soll zusammen mit Philosophie und Pädagogik bald auch in Zürich zu einem neuen Schwerpunkt für Maturanden werden. Eine gute Idee?
Nein. Da ist noch zu viel im Wandel. Solange wir Defizite haben in Mathematik und Naturwissenschaften, sollte man nicht noch mehr Fächer ins Gymnasium packen.
Sind Gymnasiasten in der Lage, interdisziplinär zu denken – so wie sich die Hochschulen das von ihren künftigen Studierenden wünschen?
Alle Menschen neigen dazu, Wissen so zu nutzen, wie sie es erworben haben – und nicht in einem anderen Kontext. Dabei ist Schulwissen dazu da, um breit aufgestellt zu sein.

Ist das schlimm?
Nein, man muss nur daran arbeiten. Im Übrigen stehen Gymnasien in der Schweiz viel besser da als in vielen anderen Ländern. Der Punkt ist: Bildung ist wie ein Garten – er kann im Frühjahr noch so schön gewesen sein, die Arbeit dazu muss bereits im Herbst gemacht werden, immer wieder. Es braucht Zeit, bis etwas Neues wächst. Und man muss sich immer überlegen, was man besser machen kann.
Was zum Beispiel?
Man sollte die jungen Leute nicht so früh dazu zwingen, sich entweder für Sprachen oder für Mathematik zu entscheiden. Diese Glaubensfrage führt dazu, dass sich gerade junge Frauen von Mathematik und Naturwissenschaften abwenden und andere Interessen entwickeln.
Auch an den Universitäten werden Mathematik und Technik weiterhin von Männern dominiert. Das ist auch ein kulturelles Problem.
Ja. Wie sind Höchstleistungen zu erklären? Frauen gelten als fleissig, Männer hingegen als brillant. Das Stereotyp, dass Frauen halt doch nicht ganz so intelligent sind wie die besten Männer und es deshalb nicht bis ganz nach oben schaffen, ist ausgeprägt. Und so werden die Leistungen von Frauen häufig übersehen. Das haben alle Frauen erlebt, die akademische Karriere machen. Und alle haben es irgendwann überwunden.
Wie war das bei Ihnen?
Ich hatte Förderer. Aber wenn ein Männergremium eine begehrte Stelle neu besetzen muss, geschieht das oft nach dem «Similar to me»-Prinzip: Männer wählen Männer, weil sie glauben, in ihnen weiterzuleben oder was auch immer. Kandidatinnen, die genauso gut sind, müssen sich nach der Absage dann Unverschämtheiten anhören wie, man sei halt eine schwierige Person. Auch das haben alle Frauen in Spitzenposition erlebt, auch ich. Und ich bin bestimmt nicht schwierig.
Sehen Sie sich als Vorbild für andere Frauen?
Ich weiss nicht, ich habe keine Kinder. Das macht vieles leichter. Aber ich habe schon relativ viele Frauen zu Professorinnen gemacht, die bereits Kinder hatten . . . Ich habe mich selber glaub nicht als Vorbild gesehen, aber vielleicht war ich’s manchmal.
Ihre wichtigste Botschaft für junge Wissenschafterinnen?
Lasst euch nicht entmutigen. Viele Frauen können nicht mit unangenehmen Situationen umgehen. Sie waren sehr gute Schülerinnen, sie hatten wenig Widerstand. Und wenn sie später mit «bösen» Männern zu tun haben, kommen sie nicht damit zurecht. Oder wenn eine Publikation abgelehnt wurde. Da gibt es nur eines: weitermachen!
Warum wollten Sie Professorin werden und nicht Lehrerin? In einem Klassenzimmer wären Sie viel näher dran am Lernen.
Ich wusste schon mit 16 Jahren, dass ich Psychologieprofessorin werden wollte. Ich wollte etwas über Intelligenz und das menschliche Denken herausfinden. Das ist der Vorteil von nichtakademischen Elternhäusern: Es redet einem niemand drein.
Lernforschung für die Lehrer
R. Sc. · Elsbeth Stern ist ordentliche Professorin für Lehr- und Lernforschung der ETH Zürich und Leiterin des Instituts für Verhaltenswissenschaften am dortigen Departement für Geistes-, Sozial- und Staatswissenschaften. Die Psychologin beschäftigt sich seit über zwanzig Jahren mit didaktischen und lerntechnischen Fragen im Mathematikunterricht und in den Naturwissenschaften. Dies unter anderem auch in einem Studiengang für angehende Gymnasiallehrer an der ETH. Am Mint-Lernzentrum der Hochschule können sich Lehrerinnen und Lehrer auch punktuell weiterbilden lassen.
Ein weiterer Schwerpunkt der 63-jährigen Deutschen ist die Intelligenzforschung. Ihr Buch «Intelligenz: Grosse Unterschiede und ihre Folgen» aus dem Jahr 2013 enthält einige deutliche Botschaften. Zum Beispiel diese: Fleiss, Disziplin und Kreativität sind kein Ersatz für Intelligenz.
* Für die zitierte Mathematikaufgabe 125 × 6,408 gibt es einen Trick. 125 = 1000 : 8, also kann man rechnen: 6,408 × 1000 : 8 = 801. Für diesen Weg gab es an der Gymiprüfung die volle Punktzahl.
Dieser Artikel istzuerst in der NZZ erschienen (24.11.21)






Wundert uns das? Nicht wirklich. Immer das Maximum rausholen, auch wenn Max oder Maxima gar nicht können (und vielleicht auch nicht wollen). Doch für Mami und Papi gibt es keine Alternativen…
Professorin Elisabeth Stern liegt falsch , denn wenn ich gefestigt im Leben stehe , kann mir keiner was weiß machen !!