Auf dem Kontinent hatte Kopfrechnen (mental calculation) Priorität, schriftliches Rechnen wurde erst im Alter von 9 Jahren eingeführt. Es wurden zwei Arten von Kopfrechnen unterschieden: mündliches Rechnen (oral arithmetic) und reines Kopfrechnen (pure mental arithmetic). Mündliches Kopfrechnen wurde zur Einführung neuer Themen verwendet. Beim mündlichen Rechnen wurde die Aufgabe (in horizontaler Form) abgelesen (Buch, Arbeitsblatt, Wandtafel) und das Resultat wurde im Kopf gerechnet. Bei neuen Operationen wurden Zwischenschritte durchgeführt.
„Mit der Einführung der Zahlen von 10 bis 20 begegnen die Kinder einer der vollkommensten Erfindungen des menschlichen Geistes, nämlich unserer Zahlenschreibweise im Zehner-Stellenwertsystem.“ (Auszug aus einem Lehrerkommentar)
Beim reinen Kopfrechen wurde die Aufgabe im Ganzklassenunterricht mündlich gestellt und die Schüler antworteten mündlich. Diese Methode wurde erst angewandt, wenn das Prinzip und die Grundlagen der Aufgabe richtig verstanden worden waren, als praktisches Üben und Trainieren des schnellen Rechnens im Kopf. Der kontinentale Ansatz sollte den Schülern helfen, mit den, reinen Zählstrategien überlegenen, mentalen Methoden vertraut zu werden. Er sollte sie befähigen, Rechenstrategien zu entwickeln und vorteilhafte Arten der Berechnung von Summen usw. zu erkennen („Nutzung vorteilhafter Rechenwege“). Solche Strategien beinhalteten folgende Methoden: a) Additionen von zweistelligen Zahlen in kleinere Schritte aufzuteilen (Beispiel: 37 + 26 = 37 + 20 + 6), b) eine Zahl zum nächsten Zehner zu ergänzen und die zweite entsprechend zu vermindern (Beispiel: 38 + 54 = 40 + 52), c) Abkürzungen (shortcuts) wie 26 + 59 = 26 + 60 – 1, d) Neuordnung in eine einfachere Reihenfolge wie 58 + 7 – 9 – 8 = 58 – 8 – 9 + 7). Das Kopfrechnen diente der Verinnerlichung des mathematischen Denkens.
 Anspruchsvolles Kopfrechnen Ende der 1. Klasse Kanton Zürich (1956)
Anspruchsvolles Kopfrechnen Ende der 1. Klasse Kanton Zürich (1956)
Bevor kontinentale Kinder in die Addition von dreistelligen Zahlen mit schriftlichem Rechnen eingeführt wurden, lernten sie die Addition im Kopf anhand einfacherer dreistelliger Zahlen, um ihr Vorstellungsvermögen für dreistellige Zahlen zu entwickeln. Auf dem Kontinent wurde gegen zu frühes schriftliches Rechnen argumentiert, dass die Aufsplittung der Zahlen (place value) dazu führen könnten, dass Zahlen nicht mehr länger als ganze Einheiten, sondern als eine Ansammlung von Ziffern wahrgenommen werden. Rechnen würde dann als reine Manipulation von Symbolen ausgeführt und trüge nicht mehr zum Verständnis von Zahlen und ihren Zusammenhängen bei, grobe Fehler würden nicht mehr erkannt.
In englischen Mathematikbüchern spielte das Kopfrechnen eine vernachlässigbare Rolle, das schriftliche Rechen mit dem vertikalen Addieren war vorherrschend und wurde auch für die Addition von zweitstelligen Zahlen angewandt.
Der Schritt-für-Schritt Ansatz
Die Sequenzierung von Übungen in den kontinentalen Schulbüchern unterstützten das Lernen der Schüler. Die Übungen waren nach Schwierigkeitsgraden geordnet: komplexe Operationen wurden in einfachere Schritte aufgebrochen, jeder Schritt wurde separat geübt, bevor sie in komplexeren Operationen angewandt wurden. Dieser abgestufte Ansatz erlaubte den Schüler sich auf nur eine neue Schwierigkeit aufs Mal konzentrieren zu müssen („Prinzip der Isolierung der Schwierigkeiten“).
Für jeden Schritt stellten die Schulbücher Aufgaben zum mündlichen Üben im Ganzklassenverband zur Verfügung und danach als individuelle schriftliche Arbeit. Die Anzahl Übungen variierten von 20 bei einfachen Schritten bis zu über 400 bei schwierigen Schritten (56 + 7 oder 56 + 37) mit Zehnerübergang. Im Nummernbereich zwischen 20 und 100 enthielt das kontinentale Schulbuch über 900 Übungsaufgaben zur Addition, während beim englischen 400 nicht überschritten wurden.
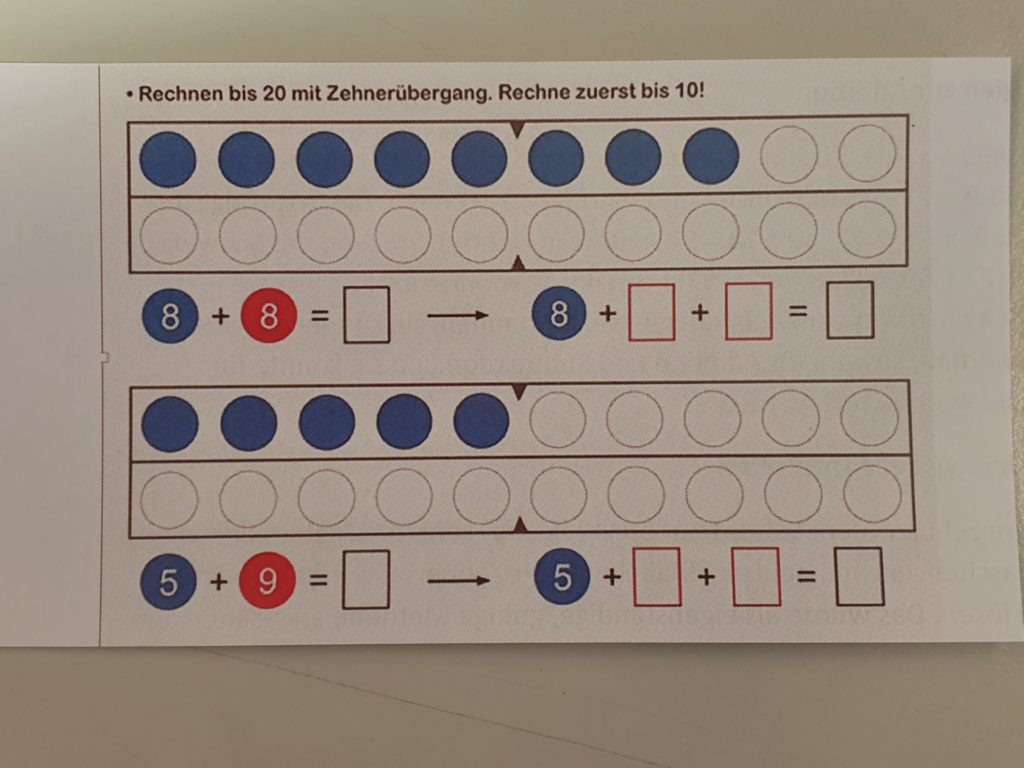
Einführung des „Zehnerübergang“ gegen Ende der 1. Klasse
In den kontinentalen Büchern wurde in sorgfältig abgestufter Weise variiert, während in den englischen Aufgaben in einem Dutzend verschiedenen Formen präsentiert wurden. Auf dem Kontinent war man der Ansicht, dass die Schüler mit einer grossen Anzahl von Variationen unnötig abgelenkt würden.
Der Schritt-für-Schritt Ansatz hatte in Deutschland und der Schweiz eine lange Tradition, bis kürzlich einige Verfechter der „Neuen Mathematik“ kritisierten, dass diese Praxis überdetailliert sei.
Der Schritt-für-Schritt Ansatz hatte in Deutschland und der Schweiz eine lange Tradition, bis kürzlich einige Verfechter der „Neuen Mathematik“ kritisierten, dass diese Praxis überdetailliert sei. Tatsache ist, dass die traditionellen Ansätze über viele Jahre auf der Basis von Erfahrung und Forschung entwickelt und verbessert wurden, während die von einigen Pädagogen als „unvergleichlich überlegen“ propagierten Alternativen, nie in grösseren Langzeitprojekten erprobt und getestet wurden.
Übung und Festigung
Im Gegensatz zum Kontinent ist die Betonung des Übens und Festigens in England unterentwickelt, sowohl in Bezug auf die Quantität als auch auf die Qualität. Für die Pädagogen auf dem Kontinent bilden üben und festigen eines neuen Themas zweierlei Zwecken: Erstens sollten die Schüler eine gründliche Vorstellung über den Zusammenhang mit früher Gelerntem erhalten und erste Erfahrungen und eine Geläufigkeit in der Anwendung des Neuen erwerben. In dieser Phase des Lernens sollten die Schüler ermutigt werden, die Operationen zu durchdenken und mit ihren logischen Grundlagen gründlich vertraut zu werden. Zweitens sollten die Schüler, nachdem sie das neue Thema gründlich verstanden und verinnerlicht hatten, genügend Übungszeit erhalten, um es mit zunehmender Leichtigkeit und Geschwindigkeit anwenden zu können. In Deutschland und der Schweiz war man der Meinung, dass die Kinder die grundlegenden Fertigkeiten „automatisieren“ müssten, um ihre Anwendung in komplexeren Verfahren und Kontexten zu erleichtern.
Alternative mentale Methoden
In Grossbritannien und auf dem Kontinent war man sich einig, dass alternative Kopfrechenmethoden nicht durch den Lehrer den Kindern aufgezwungen werden sollten. Kontinentale Lehrer ermutigten die Kinder, eigene Strategien auszuprobieren, worauf sie ihnen anschliessend effizientere Wege aufzeigten, weil es in der Verantwortung des Lehrers sei, ihnen effiziente Methoden, auch im Klassenverband, beizubringen. Im Gegensatz dazu wurde in Grossbritannien jede von den Schülern selbst erfundene Methode als akzeptabel betrachtet.
Effizienz von mentalen Strategien zur Addition
In England hatte man sich weniger um die Effizienz der mündlichen Methoden gekümmert, man verwendete die gleichen Methoden für das mündliche und schriftliche Rechnen. Die ursprüngliche Dreischrittmethode (27 + 65 = 80, 5 + 7 = 12, 80 + 12 = 92) wurde in Deutschland und der Schweiz durch die Zweischrittmethode (27 + 60 = 87, 87 + 5 = 92) ersetzt. Die kontinentale Zweischrittmethode half den Schülern von der Zählstrategie wegzukommen, sie konnte für jede zweistellige Zahl angewendet werden, sowohl für Addition und Subtraktion und sie konnte für Kalkulationen mit grösseren Zahlen erweitert werden.
Konkrete Materialien und andere visuelle Hilfsmittel
Englische Lehrer ermutigten ihre Schüler (dem Lehrerhandbuch folgend) konkrete Materialien wie ineinandergreifende Würfel, Flaschenverschlüsse, Lolly-Stäbchen oder Zehnerblöcke zu verwenden, um arithmetische Probleme zu lösen. Das wurde als eigenständige, gültige Methode angesehen, um das Resultat zu finden. Ihren eigenen Ressourcen überlassen, verwendeten englische Schüler diese Objekte oder ihre Finger auch noch im Alter von 9 bis 10 und sogar darüber. So blieben sie bei ihrer Zählstrategie anstatt Rechenstrategien zu entwickeln.
„Wird zählendes Rechnen verfestigt, stellt es eine Sackgasse dar, aus der die Schüler im 2. oder im 3. Schuljahr kaum mehr herauskommen.“ J.H. Lorenz / H. Radatz, 1993
Russische Forschung in der Zwischenkriegszeit zeigte, dass das Lernen der Schüler leidet, wenn die Phase während der sie konkretes und visuelles Material verwenden, zu lange ausgedehnt wird. Der sowjetische Psychologe und Begründer der Theorie der kulturellen und sozialen Entwicklung des Menschen Lew Wygotski stellte fest, dass die zu starke Betonung des visuellen Denkens, die kleinen Anfänge des abstrakten Denkens der älteren Schüler ersticken würden. Im Unterricht sollte versucht werden, die natürliche geistige Entwicklung von Kindern zu erweitern und zu fördern und sie über ihr bereits erreichtes Entwicklungsstadium hinauszuführen.

Neunjährige englische Schüler wurden beobachtet, wie sie einfache Aufgaben, wie 21 minus 12, mit ihren Fingern lösten, während kontinentale Schüler in diesem Alter ein sicheres Gespür für Kopfrechenstrategien für Zahlen bis 100 hatten. In England glaubte man, wenn man den Kindern genügend konkretes Material zur Verfügung stellte, würde das Verständnis für die Zahlen schliesslich von selbst kommen. Auf dem Kontinent war man der Überzeugung, dass die verlängerte Verwendung von Zählstrategien das Verständnis für die Beziehungen zwischen den Zahlen verhindern würde.
Taschenrechner

Auf dem Kontinent wurden wegen der Priorität des Kopfrechnens keine Taschenrechner vor dem 13 bis 14 Altersjahr und kaum in der Primarschule verwendet. In England wurde die Verwendung von Taschenrechnern vom Grundschulalter an gefördert und wurde Teil der gesetzlichen Anforderungen des Nationalen Lehrplanes ab dem fünften Altersjahr (Key Stage 1). In England wurde die Verwendung von Taschenrechnern als eine Form der „aktiven Beteiligung“ und des „Experimentierens“ gesehen. Auf dem Kontinent wurden Rechner als ungeeignet für den primären Mathematikunterricht erachtet, weil man mit Kopfrechnen das Verständnis der Schüler für Zahlen zu einem frühen Zeitpunkt ermöglichen wollte.

Aus Fehlern nichts gelernt
In der Schweiz beobachteten Gymnasiallehrer in den 1990er Jahren im mathematischen und naturwissenschaftlichen Bereich, dass den neu eingetretenen Schülern die Grundlagen für die gymnasialen Lehrmittel fehlten, die an sich inhaltlich und didaktisch gut waren. Bei genauerem Hinsehen zeigte sich, dass viele Schüler Lücken bei den Grundlagen aufwiesen. Sie hatten Mühe beim zehnerüberschreitenden Rechnen und konnten das Einmaleins nicht mehr. Und sie mieden deshalb später das Studium in diesen Fächern. Die MINT-Studie stellte 2010 einen eklatanten Mangel an qualifizierten Fachkräften im Bereich Mathematik, Informatik, Naturwissenschaften und Technik fest, auf die unsere Volkswirtschaft so dringend angewiesen ist.
All dies korrelierte auffallend mit der Einführung des „offeneren“, „problemorientierten“ Herangehens der „Neuen“ Mathematik-Lehrbücher (Mengenlehre usw.) von Professor Adolf Kriszten, Leiter der Arbeitsstelle Mathematik des Pestalozzianums. Die im Kanton Zürich in der Volksschule ab 1978 eingeführten, „revolutionären“ Lehrbücher „Wege zur Mathematik“ 1-6, wiesen genau die Merkmale auf, die von den britischen Wissenschaftlern bemängelt wurden. Der systematische Aufbau wurde falschen theoretischen Ideen geopfert. Die Ära der „Neuen“ Mathematik dauerte 17 Jahre mit gravierenden Folgen für diese Schülergeneration und ihre Berufskarriere.
Die Fehler der „Neuen“ Mathematik wurden von Professor dipl. math. Walter Hohl, Direktor der Sekundarlehrerausbildung an der Universität Zürich in den 1980er Jahren, wieder rückgängig gemacht. Unter seiner Leitung wurde das gut strukturierte und logisch aufgebaute Lehrmittel „Mathematik“ 1-6 geschaffen, das ab 1995 vielen Lehrern, nicht nur im Kanton Zürich, wieder einen erfolgreicheren Mathematikunterricht ermöglichte.
Es wundert wohl mittlerweile kaum jemanden, dass alle gescheiterten Elemente der „Neuen Mathematik“ und in anderen Fächern im Lehrplan 21 wieder auftauchen. Dazu kommt, dass mit dem Rückzug der Lehrer (nur noch Lernbegleiter) beim individualisierenden Lernen, der autoritäre Einfluss der kompetenzorientierten Lehrmittel verstärkt wird.
Peter Aebersold
Quellen:
Helvia Bierhoff: Laying the Foundations of Numeracy: a comparison of primary school textbooks in Britain, Germany and Switzerland. Discussion Paper no. 90, National Institute of Economic and Social Research, London January 1996.
Helvia Bierhoff, S. J. Prais: From School to Productive Work: Britain and Switzerland Compared, University Press, Cambridge 1997.






