
Drei Erfahrungsberichte aus der schweizerischen Praxis
„Acht Tennisbälle, drei Schubladen. Wie viele Verteilungen sind möglich?“
Die Maturprüfung beginnt um 8 Uhr, sie dauert 15 Minuten. Es werden zwei Themen im etwa gleichen zeitlichen Umfang geprüft. Der Schüler hat keine Vorbereitungszeit. Er betritt den Raum, wird von Prüfer und Experte knapp begrüsst, erblickt den ihm angedachten Platz, zieht seine Jacke aus und möchte sich setzen. Noch während ein Arm in der Jacke hängt, erhält er die erste, nur mündlich formulierte Aufgabenstellung: „Acht Tennisbälle werden auf drei Schubladen verteilt. Auf wie viele Arten geht das?“ Der Schüler, sichtlich erstaunt über den unvermittelten Beginn der Prüfung, befreit seinen Arm aus der Jacke und setzt sich, während er murmelnd nachdenkt: „Tennisbälle – wie viele? Und wie viele Schubladen?“ – „Acht und drei“, antwortet der Prüfer kurz und knapp, um nach nur einer Sekunde Wartezeit nachzuhaken: „In welchem Gebiet sind wir denn hier?“ – „Ich denke, es geht um Kombinatorik“, antwortet der Schüler, schafft es aber nicht, in der gegebenen Zeit von wenigen Sekunden die anfangs gestellte Frage zu beantworten.
Der Prüfling hat sich dem Fragenbombardement tapfer gestellt, aber konnte er auch zeigen, was er beherrscht?
So geht es weiter, 15 Minuten lang. Der Prüfer stellt eine Frage nach der nächsten, Zeit zum Nachdenken bleibt kaum – die Prüfungszeit sei schliesslich knapp und es solle doch so viel wie möglich abgeprüft werden, so die später vorgebrachte Begründung des Prüfers für die schnelle Abfolge der vielen Fragen. Für den Prüfling, der mit jeder Frage nervöser zu werden schien, gibt es am Ende eine knapp genügende Note. Er hat sich dem Fragenbombardement tapfer gestellt, aber konnte er auch zeigen, was er beherrschte?
Im Rückblick erscheint die Prüfung als eine gewaltige Stresssituation für alle: Der Prüfer formulierte, getrieben von der tickenden Uhr, eine Frage nach der anderen, in der Überzeugung, nur so das Wissen des Prüflings angemessen einschätzen und bewerten zu können. Der Prüfling versuchte, so gut es ging, auf die Flut an Fragen und Aufgaben zu reagieren. Zeit zum Nachdenken und Argumentieren blieb kaum. Er musste, so schnell es geht, reagieren und wurde ebenso schnell unterbrochen, wenn seine Antwort nicht genau dem entsprach, was vom Prüfer intendiert war. Schliesslich war die Situation auch für den Experten überaus anspruchsvoll: Er kannte die Fragen nicht, hörte sie im selben Moment wie der Prüfling, musste Frage und Antwort angemessen protokollieren und gleichzeitig einschätzen, inwieweit die gegebene, teils unfertige Antwort korrekt war. Das Tempo der gestellten Fragen und Aufgaben war indes so hoch, dass ein angemessenes Protokollieren nahezu ausgeschlossen war.
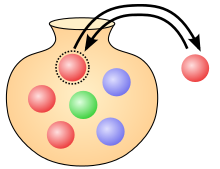
Was ist in dieser Prüfung nun tatsächlich geprüft worden? Betrachten wir die Einstiegsfrage zunächst fachlich. Die Frage, auf wie viele Arten acht (nicht unterscheidbare) Tennisbälle auf drei (unterscheidbare) Schubladen verteilt werden können, zielt auf das Urnenmodell in der Kombinatorik. Bei diesem Modell handelt es sich um ein wirksames Instrument zur Lösung von Zählproblemen, die – wie in diesem Fall – durch Enumeration, d.h. durch Abzählen und Auflisten, nicht oder nur sehr aufwendig zu lösen sind. Die Grundidee ist, das jeweilige Problem in ein Modell zu übersetzen, bei welchem aus einem Gefäss (einer Urne), das n (unterscheidbare) Kugeln enthält, k Kugeln gezogen werden. Eine mögliche Übersetzung für den hier gegeben Fall wäre die folgende: Aus einer Urne mit drei unterscheidbaren, d.h. bspw. nummerierten Kugeln, welche den drei Schubladen entsprechen, wird achtmal eine Kugel gezogen. Nach jedem Zug wird die Nummer der Kugel notiert, bevor sie zurück in die Urne gelegt und ein weiteres Mal eine Kugel gezogen wird. So erhält man schliesslich eine achtstellige Zahl, etwa 11322312, welche einer möglichen Verteilung der Kugeln entspricht – in diesem Fall lägen in der ersten Schublade drei, in der zweiten ebenfalls drei und in der dritten Schublade zwei Tennisbälle, was einer möglichen Verteilung der Bälle entspricht. Von den vier möglichen Fällen, die das Urnenmodell umfasst, handelt es sich also um eine „Kombination mit Wiederholung“ („Kombination“, da die Reihenfolge der gezogenen Kugeln nicht relevant ist, „mit Wiederholung“, da eine Kugel mehrfach gezogen bzw. eine Schublade mehr als einen Ball aufnehmen kann). Mit der entsprechenden Berechnungsformel lässt sich nun ermitteln, dass insgesamt 45 solcher Verteilungen möglich sind.
Die im ersten Moment harmlos klingende Frage beinhaltet zahlreiche zu bewältigende Schwierigkeiten.
Diese Überlegungen hätte der Prüfling wohl so oder so ähnlich in der Prüfung verbalisieren sollen. Dazu braucht es Ruhe und Zeit. Zunächst muss erkannt werden, in welchem Teilgebiet der Mathematik man sich befindet (Kombinatorik). Dann müssen die für die Fragestellung relevanten Inhalte dieses Teilgebiets identifiziert werden (vier Fälle des Urnenmodells), schliesslich müssen die gegebenen Informationen analysiert werden, um den entsprechenden Fall auswählen (Kombination mit Wiederholung) und die Berechnung durchführen zu können (45 Verteilungen). Es gibt zahlreiche Stellen, an denen man falsch abbiegen kann. So ist bspw. eine entscheidende Information, dass nämlich die Bälle nicht, die Schubladen aber sehr wohl unterscheidbar sind, vom Prüfer gar nicht genannt worden – eine zusätzliche Schwierigkeit. Dann wäre es naheliegend, nicht die Schubladen, sondern die Bälle in die Urne zu legen und diese nacheinander zu ziehen. Erst wenn man das Urnenmodell für diesen Fall durchdenkt, erkennt man, dass auf diese Weise jedoch nicht entschieden werden kann, welcher Ball in welche Schublade gelegt werden soll. Der Fehler liegt also nicht auf der Hand, ihn zu erkennen braucht wiederum Zeit. Schliesslich muss für die Berechnung auch noch die entsprechende Berechnungsformel, die nicht ohne weiteres herzuleiten ist, angewendet werden. Da die vier Formeln des Urnenmodells recht ähnlich sind, besteht hier die Gefahr, diese im Prüfungsstress durcheinander zu bringen. Kurzum: Die im ersten Moment harmlos klingende Frage beinhaltet zahlreiche zu bewältigende Schwierigkeiten.
Die Frage ist als Einstieg in eine Prüfung, zu der es keinerlei Vorbereitungszeit gab, schlichtweg ungeeignet.

Unter welchen Rahmenbedingungen wäre es für einen Prüfling möglich, den oben skizzierten Gedankengang in einer mündlichen Prüfung zu entwickeln, und welche alternativen Einstiege in die Prüfung sind denkbar, wenn kombinatorisches Wissen geprüft werden soll? Zum ersten beginnt die Prüfung völlig unvermittelt. Die Prüfungssituation ist noch gar nicht hergestellt, der Prüfling richtet sich noch ein, sitzt noch nicht am Tisch, als die erste Frage gestellt wird. Ein solcher Beginn vermindert die Objektivität der Prüfung, was auch für die Tatsache gilt, dass ein angemessenes Erstellen des Prüfungsprotokolls bei einer so hohen Fragedichte kaum möglich ist. Es kann keine Ruhe einkehren, der hektische Einstig zerstört schon zu Beginn eine angemessene Prüfungsatmosphäre. „Eile verdirbt alles“ (Wagenschein 1976, S. 106). Zum zweiten ist die Einstiegshürde fachlich gesehen sehr hoch: Bei dem Fall „Kombinatorik mit Wiederholung“ handelt es sich erfahrungsgemäss um den schwierigsten der vier Fälle des Urnenmodells. Möglicherweise, weil die Herleitung der entsprechenden Berechnungsformel im Gegensatz zu den übrigen drei Formeln einen schwer nachvollziehbaren, nur hier anwendbaren Trick beinhaltet,[1] vielleicht, weil es zunächst nicht naheliegend zu sein scheint, Schubladen statt Tennisbälle aus der Urne zu ziehen. Kurzum: Die Frage ist als Einstieg in eine Prüfung, zu der es keinerlei Vorbereitungszeit gab, schlichtweg ungeeignet.
Ist keine Vorbereitungszeit vorhanden, muss die Prüfung mit einer möglichst kleinen Hürde beginnen.
Kann der Prüfling die Frage beantworten, zeugt das nicht zwangsläufig von einem hohen Kenntnisstand, schlimmer: Kann sie oder er sie nicht beantworten, kann keineswegs gefolgert werden, dass die Kenntnisse im Bereich der Kombinatorik mangelhaft sind. Mit grosser Wahrscheinlichkeit ist daher mindestens dieser Teil der Prüfung, möglicherweise sogar die Prüfung in toto nicht valide. Natürlich ist es nicht ausgeschlossen, im Laufe der Prüfung – nicht zu Beginn – zu einer Frage wie der genannten zu kommen. Die erste Möglichkeit besteht in der Einrichtung einer ausreichenden Vorbereitungszeit, in welcher der Prüfling den oben skizzierten Lösungsweg entwickeln und mit mehr Ruhe durchdenken kann. Ist keine Vorbereitungszeit vorhanden, muss die Prüfung mit einer möglichst kleinen Hürde beginnen, etwa: „Mit welcher Art von Problemen beschäftigt sich die Kombinatorik?“ – „Ein wichtiges Modell in der Kombinatorik ist das Urnenmodell. Erläutern Sie dessen Grundidee.“ Oder: „Wählen Sie einen Fall des Urnenmodells aus und erläutern Sie diesen an einem selbstgewählten Beispiel“. Von diesen Fragen ausgehend kann, anschliessend an die Antworten des Prüflings, ein Gespräch entwickelt werden, bei welchem auch die Frage nach den Tennisbällen und den Schubladen angesprochen werden könnte, bei dem aber vor allem das Gebiet der Kombinatorik so durchstreift wird, dass am Ende das Wissen des Prüflings (und nicht dessen Nicht-Wissen) sichtbar werden kann, was sowohl der Validität als auch der Fairness zuträglich wäre.
„Es hat zwei Aufgaben. Lesen Sie mal und fangen Sie dann einfach an.“
Geprüft wird eine Abschlussklasse der FMS (Fachmaturitätsschule, die Abschlussprüfungen finden am Ende der 10. Klasse statt, der Abschluss entspricht in Deutschland der Mittleren Reife). Das Prüfungsarrangement sieht vor, dass die Prüflinge zu Beginn einer Prüfung zwei voneinander unabhängige Aufgaben – bei mindestens einer Aufgabe handelt es sich um eine reine Rechenaufgabe – erhalten, die sie vorher nicht kannten und auf die sie spontan reagieren müssen, da es keine Vorbereitungszeit gibt. Als Hilfsmittel zur Verfügung stehen eine Formelsammlung und ein Taschenrechner. Die Themen, die geprüft werden, sind per Zufallsprinzip auf die Prüflinge verteilt. Es geht ums lineare Gleichungssystem, um Prozentrechnung, den Satz des Pythagoras, Proportionalität, Kreisberechnung, lineare Funktionen sowie einfache Exponentialfunktionen. Jede Prüfung beginnt mit der Aushändigung des Prüfungsblatts, welches beide Aufgaben enthält. Der Prüfer kommentiert dies stets mit demselben Satz: „Es hat zwei Aufgaben. Lesen Sie beide mal durch und fangen Sie dann einfach an.“
Der Prüfer kommentiert: „Bis jetzt höre ich nur die Vögel zwitschern.“
Es folgt Stille. Für jede Prüfung ist eine Dauer von 15 Minuten vorgesehen. Mindestens die ersten zwei Minuten werden jedoch vom Prüfling dazu benötigt, beide Aufgaben zu lesen, Text und etwaige Graphiken zu verstehen, die Thematik einzuordnen, Lösungsansätze zu entwickeln. Dieser Prozess nimmt selbstredend einige Zeit in Anspruch, was der etwas ungeduldige Prüfer bisweilen mit Sätzen wie diesem kommentiert: „Bis jetzt höre ich nur die Vögel zwitschern.“ Nach einer ersten Orientierungsphase beginnen die Prüflinge damit, die Aufgabe zu lösen. Versuchen sie dies schweigend, werden sie vom Prüfer aufgefordert, „laut zu denken“. Meist versuchen die Prüflinge direkt, die Angaben aus der Aufgabe in eine Gleichung zu übersetzen. Dies ist sinnvoll, gelingt aber nicht immer problemfrei, so dass sich der Prüfer dazu angehalten sieht, auch jeden noch so kleinen Fehler, bspw. ein im Prüfungsstress vergessenes Vorzeichen, in einem sehr kleinschrittigen Gespräch vom Prüfling selbst entdecken und korrigieren zu lassen. Eine fehlerfreie und vom Prüfling korrekt notierte Rechnung am Ende der 15 Minuten scheint oberstes Ziel zu sein. Dazu verlangt der Prüfer sogar, Ausdrücke mit dem Taschenrechner auszurechnen („Tippen Sie es mal ein“) und auf zwei Nachkommastellen runden zu lassen. Dass die ungerundeten Ausdrücke das Resultat viel genauer angeben als die Dezimalzahlen, scheint für den Prüfer weniger Gewicht zu haben als die vermeintliche Kompetenz aufseiten des Prüflings, den Taschenrechner korrekt bedienen zu können.
Vorbereitungszeit würde dazu führen, dass die Prüfungszeit deutlich effizienter genutzt werden könnte.
Der Ablauf einer solchen Prüfung wirft eine Reihe von Fragen auf. So ist es bspw. unklar, warum es zu Beginn wichtig sein soll, dass die Prüflinge zwei Aufgaben direkt erhalten, wo doch nur mit einer begonnen werden kann. Es scheint, als solle dem Prüfling die Auswahl überlassen werden und die Reihenfolge der Bearbeitung nicht vom Prüfer selbst festgelegt werden. Dies entspricht dem Sachverhalt bei einer schriftlichen Prüfung, in welcher die Aufgaben prinzipiell in jeder beliebigen Reihenfolge bearbeitet werden können. Auch in einer mündlichen Prüfung kann dies aus psychologischen Gründen sinnvoll sein, sofern für eine angemessene Sichtung und Abwägung ausreichend Zeit zur Verfügung stünde. Dies ist jedoch nicht der Fall, was die nächste Frage aufwirft: Warum haben die Prüflinge keine Zeit, sich auf die Prüfung vorzubereiten? Es ist unklar, warum nicht jeder Prüfling zunächst 15 Minuten Zeit erhält, um die Aufgaben zu sichten, Lösungsansätze zu entwickeln, sich die geprüfte Thematik in Erinnerung zu rufen. Natürlich würde dies dazu führen,

dass die Prüfungszeit deutlich effizienter genutzt werden könnte: Die stillen Minuten zu Beginn würden entfallen, ein Lösungsansatz wäre schon entwickelt und könnte unmittelbar diskutiert werden, Zeit zum Nachschlagen von Formeln und dem Berechnen von Lösungen mit dem Taschenrechner entfiele, so dass insgesamt ein Teilgebiet geprüft werden könnte, das für das gesamte Gebiet oder gar die gesamte unterrichtete Mathematik deutlich repräsentativer wäre, als es in einem Arrangement ohne Vorbereitungszeit der Fall ist. Die Validität der Prüfung, deren Berücksichtigung primäres Ziel sein sollte, würde enorm steigen. Denn insgesamt stellt sich natürlich die grundlegende Frage, was ein Prüfling in einer Prüfung, die wie oben geschildert abläuft, eigentlich zeigen konnte, was er hätte zeigen können und was genau geprüft worden ist. Wie ist es bspw. zu bewerten, wenn ein Schüler es schafft, im gesamten ersten, fast zehn Minuten dauernden Teil der Prüfung nur den Umfang eines Halbkreises mit dem Radius zu berechnen? Sollte die Tatsache, dass am Ende eine korrekte, auf zwei Nachkommastellen gerundete Lösung auf dem Blatt steht, nicht in Relation gesetzt
werden mit dem Sachverhalt, dass das Entwickeln dieser sehr simplen Rechnung rund zehn Minuten in Anspruch genommen hat? Die Grundfragen der Thematik wurden damit nicht berührt, stattdessen wurde ein so kleiner, noch dazu recht unbedeutender Ausschnitt des Themas Kreisberechnung behandelt, dass eine Aussage darüber, ob und wenn ja, inwieweit der Schüler sich in dieser Thematik bewegen kann, eigentlich nicht getroffen werden kann. Die Validität der Prüfung steht damit massiv infrage und die Bewertung einer solchen Prüfung wird zu einem gewaltigen Problem.
„Ich habe für Sie das Thema X ausgesucht. Wollen Sie mal starten?“
Die zu prüfende Maturklasse besteht aus 22 Schülerinnen und Schülern. Sie haben keine Vorbereitungszeit, haben keinerlei Schwerpunkte für die Prüfung wählen können, „sie müssen alles können und mit allem rechnen“, kommentiert der Prüfer vor Beginn der ersten 15-minütigen Prüfung das Arrangement lakonisch. Ich fühle mich erinnert an einen meiner alten Chemie-Professoren aus dem Studium, der vor einer Prüfung auf die Bitte nach einer etwas konkreteren Angabe der Lernziele folgendermassen reagierte: „Lernen Sie alles, vergessen Sie nichts.“
Die Unterbrechung ist nur dann logisch, wenn der Prüfer eine ganz konkrete Sache im Kopf hat, auf die er hinaus möchte.
Die erste Prüfung startet nach einer kurzen Begrüssung, als alle Platz genommen haben. Sie wird eröffnet mit der Frage: „Ich habe für Sie das Thema Integralrechnung ausgesucht. Wollen Sie mal starten?“ Die Schülerin beginnt: „In der Integralrechnung geht es um Flächen –“, kann den Satz aber nicht vervollständigen, da sie vom Prüfer unterbrochen wird: „Um was für Flächen? Etwas genauer bitte.“ Sie kontert: „Um Flächen unter Kurven.“ – „Jetzt aber mal konkret“, fordert der Prüfer auf, als sei bisher schon sehr viel Unkonkretes geäussert worden. Unklar bleibt daher, an welcher Stelle der von der Schülerin geäusserte Halbsatz nun konkretisiert werden soll. Der spontane Antwortversuch der Schülerin wird nach nur wenigen Worten vom Prüfer unterbrochen – wie hätte sie antworten sollen, um nicht unterbrochen zu werden? Die Unterbrechung ist nur dann logisch, wenn der Prüfer eine ganz konkrete Sache im Kopf hat, auf die er hinaus möchte, einen bestimmten Teilbereich, ein Stichwort, und er schon nach nur sieben Wörtern bemerkt, dass dieses Ziel nicht erreichbar ist. Das Thema Integralrechnung ist allerdings so gross, dass es als äusserst unwahrscheinlich erscheint, als dass der Prüfling hier auf Anhieb das richtige Stichwort liefern wird. In jedem Fall ist die Unterbrechung zu einem derart frühen Zeitpunkt psychologisch äusserst ungeschickt, und sie ist auch fachlich nicht zu rechtfertigen, der Antwortversuch der Schülerin war nämlich durchaus vielversprechend. Zudem: Wenn die Prüfung doch in Wahrheit gar nicht so offen ablaufen wird, wie die Eröffnungsfrage suggeriert, und stattdessen auf einen ganz bestimmten Sachverhalt hinauslaufen soll, warum beginnt die Prüfung dann nicht gleich mit diesem?
Die Reliabilität der Einstiegsfrage steht massiv infrage, da eine unüberblickbare Vielzahl an Antworten möglich ist – wie soll man das bewerten?

Die erwähnte Eröffnungsfrage gehört an diesem Tag zum festen Ritual einer jeden Prüfung. Immer ist dies der erste Satz: „Ich habe für Sie das Thema X [Integralrechnung, Kombinatorik, Folgen und Reihen, Trigonometrie usf.] ausgesucht. Wollen Sie mal starten?“ Benevolent könnte man konstatieren, dass diese Art der Eröffnung eine völlige Offenheit signalisiert. Das Gebiet, über das nun gesprochen werden soll, möge vom Prüfling doch erst einmal oberflächlich beschritten werden. Es wäre aber auch möglich, sofort eine Besonderheit oder eine Verbindung zu einer anderen Thematik zu erwähnen und über diese zu sprechen, ebenso könnte ein eigenes Beispiel konstruiert werden, welches etwas Wesentliches des entsprechenden Themas illustriert – die Formulierung „wollen Sie mal starten“ würde wörtlich verstanden gar eine Verneinung samt Bitte zulassen, das Themengebiet zu wechseln: „Nein, lieber nicht dieses Thema, ich würde lieber über Y reden.“ In jedem Fall wird augenscheinlich die Steuerung der Prüfung in die Hände des Prüflings gelegt. Das ist sicherlich gut gemeint, doch der Volksmund weiss, dass „gut gemeint“ in der Regel das Gegenteil von „gut“ ist. Die Reliabilität der Einstiegsfrage steht massiv infrage, da eine unüberblickbare Vielzahl an Antworten möglich ist – wie soll man das bewerten? In diesem konkreten Fall kann der Prüfer zudem das anfängliche Versprechen eines offenen Einstiegs in die Prüfung kein einziges Mal einhalten. Denn er hat bei dieser Frage immer schon einen konkreten Sachverhalt im Kopf, über den er gerne sprechen möchte. Dies führt dazu, dass der erste Teil eines Antwortversuchs unmittelbar unterbrochen wird, wenn dieser nicht in die gewünschte aber vom Prüfling nicht vorhersehbare Richtung geht. Das gelingt eigentlich nie, so dass jeder Prüfling nach meist nur einem halben Satz mit weiteren Fragen konfrontiert wird. Kein Prüfling kann auch nur einen vollständigen Gedanken formulieren, ohne unterbrochen zu werden. Es ist eine bekannte Faustregel für Interviews jeglicher Art: Je konkreter die Frage, desto konkreter die Antwort. Umgekehrt heisst dies, dass eine offene Frage immer nur unkonkret beantwortet werden kann, da man sich für eine Antwort entscheiden muss und immer unendlich viele andere Dinge nicht gesagt werden können. Gerade dieser Umstand macht das Beantworten einer offenen Frage auch zu einer anspruchsvollen Aufgabe, insb. dann, wenn seitens des Prüfers ohnehin eine spezielle Antwort gewollt ist und eigentlich kein echtes Interesse an der Antwort besteht. Die Chance, dass die gegebene Antwort die Prüfung in die vom Prüfer intendierte Richtung lenkt, ist verschwindend gering.
Natürlich kann eine Prüfung durchaus mit einer offenen Frage beginnen. Dies setzt allerdings zwei Dinge voraus: erstens ein ehrliches Interesse an der gegebenen Antwort, auf der das weitere Prüfungsgespräch aufbauen soll, und zweitens das Vorhandensein von weniger Prüfungsdruck und ausreichend Zeit.
Abermals fragen wir nach möglichen alternativen Prüfungsarrangements: In einer Pause konfrontiere ich den Prüfer mit meiner Beobachtung und bringe die Option ein, die erste, offene Frage auszulassen und stattdessen mit einer sehr viel konkreteren Frage zu beginnen, immerhin wisse er doch schon, auf welchen konkreten Sachverhalt die Prüfung hinauslaufen solle. Der Kern der Prüfung stehe doch bereits fest, warum diesen also nicht gleich zu Beginn offenlegen? Der Prüfer ist nicht überzeugt und bleibt bei seiner Art, die Prüfungen zu beginnen. Und natürlich kann eine Prüfung durchaus mit einer offenen Frage beginnen. Dies setzt allerdings zwei Dinge voraus: erstens ein ehrliches Interesse an der gegebenen Antwort, auf der das weitere Prüfungsgespräch aufbauen soll, und zweitens das Vorhandensein von weniger Prüfungsdruck und ausreichend Zeit. D.h. dass auch in diesem Fall das Einrichten einer Vorbereitungszeit die Validität der Prüfung steigern könnte, was darüber hinaus auch aus pädagogischen und psychologischen Gründen sinnvoll wäre. Denn eine Frage wie die folgende unvorbereitet und zufriedenstellend zu beantworten, dürfte auch für viele Mathematik-Lehrpersonen eine Herausforderung sein: „Erläutern Sie den Kern der Integralrechnung an einem geeigneten Beispiel.“
Kernprobleme
- Fehlende Übung der Prüfenden
Die gesetzlichen und schulischen Vorgaben zur Abnahme mündlicher Prüfungen legen die vor allem juristisch relevanten Rahmenbedingungen fest. Werden diese eingehalten, wird die Chance eines etwaigen Rekurses seitens des Prüflings minimiert. Dieser Fakt ist daher insb. für die Prüfenden und die Prüfungsleiter, d.h. in der Regel die Schulleiter, ein entscheidendes Kriterium, es ist aber kein pädagogisches. Denn das Ziel einer fairen und gerechten Prüfung ist damit bei weitem noch nicht erreicht, wie die drei Beispiele im vorhergehenden Abschnitt zeigen: Alle drei haben die jeweils gegebenen Rahmenbedingungen berücksichtigt.
Es ist nichts anderes als eine Zumutung, dass eine Schülerin, ein Schüler, nur ein einziges Mal in ihrem bzw. seinem Schulleben eine mündliche Mathematikprüfung ablegen muss, bei der es sich auch noch um die Abschlussprüfung handelt.
Insb. in den Sprachfächern ist das Durchführen mündlicher Prüfungen eine Selbstverständlichkeit. Lehrpersonen, die regelmässig mündliche Prüfungen abnehmen, befassen sich praktisch ununterbrochen mit den Schwierigkeiten und Chancen dieser Prüfungsart. Gleichzeitig ist eine mündliche Matur- bzw. Abiturprüfung für die Prüflinge in diesen Fächern schlichtweg eine weitere mündliche Prüfung, wenngleich ihre Bedeutung im Vergleich zu einer regulären Prüfung im laufenden Schuljahr natürlich höher einzuschätzen ist. In Mathematik verhält es sich jedoch völlig anders: Mündliche Prüfungen stellen hier eine grosse Ausnahme dar. Es ist nichts anderes als eine Zumutung, dass eine Schülerin, ein Schüler, nur ein einziges Mal in ihrem bzw. seinem Schulleben eine mündliche Mathematikprüfung ablegen muss, bei der es sich auch noch um die Abschlussprüfung handelt. Dies zu betonen scheint redundant, aber es ist der bedauerliche Normalfall.
Dabei ist es Mathematiklehrpersonen nicht untersagt, auch im regulären Unterricht gewisse Themengebiete mündlich zu prüfen. Auch besteht die Möglichkeit, die Schülerinnen und Schüler wählen zu lassen, ob sie zu einem bestimmten Thema entweder mündlich oder schriftlich geprüft werden möchten. Beides geschieht allerdings höchst selten. Die klassische schriftliche Prüfung am Ende eines Themas ist nach wie vor der Normalfall. Daher ist es auch nur folgerichtig, dass sich Lehrpersonen, die – sofern sie eine Abschlussklasse unterrichten – nur einmal im Schuljahr eine mündliche Prüfung abnehmen, mit den Gütekriterien mündlicher Prüfungen kaum auseinandersetzen. Der Bedarf fehlt. Dies generiert nun aber offenkundig einen entsprechenden Weiterbildungsbedarf.
- Fehlende Vorbereitungszeit für die Geprüften
Ausgehend von der Annahme, dass Fairness das anzustrebende Ideal einer jeden Leistungsüberprüfung ist, dass diese eine gerechte Beurteilung von Lernerfolgen zum Ziel hat und dass auch eine mündliche Prüfung die Leistung der Geprüften gültig, zuverlässig und objektiv abbilden muss, stellt sich die Frage, ob die Einrichtung einer Vorbereitungszeit auch bei einer mündlichen Maturprüfung hilfreich sein könnte. Dass dies im Fach Mathematik in der Schweiz nicht der Normalfall ist – in anderen Fächern ist die Vorbereitungszeit sakrosankt, in Deutschland auch in Mathematik sogar gesetzlich vorgeschrieben – ist oben bereits angesprochen worden. Doch gibt es auch inhaltliche Argumente?
Die Note ist nicht Kern der Prüfung, sie ist deren numerisches Resultat, das am Ende ermittelt werden muss, ob man will oder nicht. Eigentlich geht es um etwas anderes: Gültigkeit, Zuverlässigkeit, Objektivität und damit zusammenhängend Fairness, Gerechtigkeit, Gleichbehandlung.
Wenn sich ein Prüfling 15 oder 20 Minuten lang auf eine mündliche Prüfung vorbereiten kann, minimiert dies den Prüfungsstress, sofern die ihm gestellten Aufgaben klar formuliert sind, deren Anzahl insgesamt nicht zu hoch ist und mindestens die Einstiegsaufgabe ein niedriges bis mittleres Schwierigkeitsniveau hat. Der Prüfling hat Zeit, sich auf das Fach und das entsprechende Teilgebiet einzulassen, kann in der Formelsammlung blättern und gewisse Schwerpunkte rekapitulieren. Die Prüfung kann mit der Darlegung seiner Überlegungen beginnen, er kann, sofern die Aufgabenstellung dies zulässt, die Schwerpunkte selbst setzen, indem er bspw. mit eigenen Beispielen einen Sachverhalt erläutert, die ihrerseits anschlussfähig sind für das weitere Prüfungsgespräch. Die Validität der Prüfung steigt. Natürlich bleibt die Leitung der Prüfung in den Händen der prüfenden Lehrperson, wenngleich das Führen eines solchen Prüfungsgesprächs anspruchsvoller sein dürfte als die Durchführung einer Prüfung mit mehrheitlich abfragendem Charakter. Ein häufiges Gegenargument ist, dass im Gegenteil die Vorbereitungszeit den Prüfungsstress erhöhen könnte, wenn bspw. die Aufgabenstellung vom Prüfling nicht oder nur unzureichend verstanden wird. Diese Gefahr besteht zweifelsfrei, jedoch wäre in einem solchen Fall auch die Aufgabenstellung nicht unschuldig, da möglicherweise die Einstiegshürde zu hoch ist. Ein Auftrag wie „beschreiben Sie das Diagramm“ – nicht: „interpretieren Sie“ – darf einen Maturanden, eine Maturandin nicht überfordern. Die Einstiegsaufgabe muss immer so formuliert sein, dass sie von jedem Prüfling in der Vorbereitungszeit verstanden und bearbeitet werden kann. Ein weiteres Gegenargument könnte sein, dass es keine Evidenz dafür gibt, dass die Prüfungen durch die Einrichtung einer Vorbereitungszeit besser würden. Das könnte tatsächlich sein, doch geht dieses Argument am Kern der Sache vorbei. Denn die Beurteilung steht nicht im Zentrum. Die Note ist nicht Kern der Prüfung, sie ist deren numerisches Resultat, das am Ende ermittelt werden muss, ob man will oder nicht. Eigentlich geht es um etwas anderes: Gültigkeit, Zuverlässigkeit, Objektivität und damit zusammenhängend Fairness, Gerechtigkeit, Gleichbehandlung. Diese Dinge werden durch den Verzicht auf eine Vorbereitungszeit praktisch ignoriert, der Fokus liegt dann vor allem auf dem Resultat sowie der scheinbar bequemeren Prüfungsvorbereitung und -durchführung. Das Ideal Fairness rückt in weite Ferne.
Ausblick
Es soll an dieser Stelle nicht verschwiegen werden, dass der Schreibende in den rund 250 Maturprüfungen, die er als Experte begleiten durfte, sowie in den rund 120 Diplomprüfungen, auch sehr gelungene Prüfungen beobachten konnte: Eine Lehrerin etwa, welche die wichtigsten Fragestellungen wie in einem Leitfadeninterview notiert hatte und diese dem Prüfling im Verlauf des Prüfungsgesprächs vorlegte, so dass sich auf Basis dieser Fragen ein angenehmes, fast schon lockeres und doch ernstes Gespräch entwickeln konnte. Der Prüfling konnte zeigen, was er wusste, die Lehrerin reagierte behutsam auf die Äusserungen, korrigierte nur, wo es unbedingt nötig war und brachte von Zeit zu Zeit einen neuen Aspekt in das Thema ein. Diese Art der Prüfung gelang sowohl bei den starken als auch bei den eher schwachen Prüflingen, weil das Niveau der Prüfungen diesen entsprach und bei Bedarf im Verlauf des Gesprächs angepasst wurde, was pädagogisch und psychologisch in hohem Masse sinnvoll ist. Bei der Bewertung orientierte sie sich an einem Raster der erwartbaren Antworten, welches sie für jede Prüfung vorbereitet hatte. Es gibt alles in allem keine Gründe daran zu zweifeln, dass diese Prüfungen gültig, zuverlässig und objektiv durchgeführt wurden.
Hoffnung macht das Projekt „Weiterentwicklung der gymnasialen Maturität“ (WEGM).
Sicherlich gibt es weitere gelingende Prüfungskonzepte, die an der ein oder anderen Schule von diversen Lehrpersonen im Fach Mathematik durchgeführt werden. Das mit grossem Abstand am häufigsten anzutreffende Konzept ist hingegen das oben beschriebene, welches nicht selten zu Entwicklungen führt, die in den drei Erfahrungsberichten angesprochen wurden und in höchstem Masse zu kritisieren sind. Eine Abkehr von dieser Art der Maturprüfungen im Fach Mathematik scheint aus vielerlei Gründen angezeigt.
Hoffnung macht das Projekt „Weiterentwicklung der gymnasialen Maturität“ (WEGM), welches in der Schweiz 2018 angelaufen ist und sich bis Ende September 2022 in der Vernehmlassung befindet. Gegenstand der Vernehmlassung ist der Revisionsentwurf der Verordnung über die Anerkennung von gymnasialen Maturitätsausweisen (Maturitäts-Anerkennungsverordnung, MAV) vom 15. Februar 1995 und der Verwaltungsvereinbarung zwischen dem Schweizerischen Bundesrat und der Schweizerischen Konferenz der Kantonalen Erziehungsdirektoren (EDK) über die Anerkennung von Maturitätszeugnissen vom 16. Januar/15. Februar 1995. Die existierenden Vorlagen sehen eine Reihe von teils radikalen Reformen vor, sie betreffen u.a. eine Erweiterung des Fächerkatalogs, eine Erweiterung der Maturprüfungsfächer, eine mögliche Anpassung der Bestehensnorm, die Einführung einer Prüfung zur „Zulassung zur Maturität“ – insgesamt erscheinen die Vorschläge eine noch stärkere Atomisierung der Bildung zu begünstigen.[2] Eine zukunftsweisende Weiterentwicklung dürfte anders aussehen. Die Prüfungsform etwa wird nicht angesprochen. Weder wird die Möglichkeit diskutiert, bestimmte Fächer schriftlich oder mündlich zu prüfen, noch gibt es Überlegungen bzgl. der Rahmenbedingungen zur Durchführung mündlicher Prüfungen an sich. Vielleicht sollen Entscheidungen wie diese ja auch in die Hoheit der Kantone gelegt werden. Die Hoffnung stirbt bekanntermassen zuletzt – aber sie stirbt.
[1] „An idea which can be used only once is a trick. If you can use it more than once it becomes a method.” (Polyà/Szegö 1972, viii)
[2] Bei der genauen Lektüre der vorgeschlagenen Änderungen fühlt man sich erinnert an eine Passage aus dem Bericht „A Nation at Risk“ (ANAR; 1989), der in den USA als Antwort auf die Ende der 1980er Jahre immer lauter werdenden Rufe nach einer umfassenden Schulreform geschrieben worden ist. Er fasst die damalige Situation knapp, prägnant und gut verständlich zusammen und gilt heute als Beginn der standardbasierten Schulreform (vgl. Gerwig 2017). Die in dem Bericht vorgeschlagenen Massnahmen waren allerdings vor allem pädagogischer Natur, die mit den später tatsächlich umgesetzten und in dem Gesetz „No Child Left Behind“ (2001) festgeschriebenen Massnahmen, die auch die Schulentwicklungen in Deutschland und der Schweiz massiv beeinflussten, nur noch wenig zu tun haben. In ANAR heisst es: „Secondary school curricula have been homogenized, diluted, and diffused to the point, that they no longer have a central purpose. In effect, we have a cafeteria-style curriculum in which the appetizers and desserts can easily be mistaken for the main courses.“ (NCEE 1983, S. 18)







Es ist äusserst wohltuend, wie exakt Herr Gerwig die Situationen beschreibt und was zu beachten wäre.
Worauf am Schluss verwiesen wird, dürfte eine Weiterentwicklung anders von statten gehen. Die EDK har in den vergangenen 30 Jahren genug Schlamassel angerichtet aus Unkenntnis, worauf es beim Unterrichten ankommt als Grundlage für allfällige Prüfungen.
Guten Tag
Ich möchte darauf aufmerksam machen, dass Fachmaturitätsprüfungen nicht am Ende der 10. Klasse stattfinden. Eine Fachmittelschule dauert drei Jahre und wird (theoretisch) direkt im Anschluss an die 9. Klasse begonnen und daher in der 10., 11. und 12. Klasse besucht. Ob die Fachmaturitätsprüfung am Ende der 12. Klasse oder sogar (ein Jahr?) später absolviert werden, weiss ich nicht. (Die Reihenfolge lautet auf gar keinen Fall “erst Fachmaturität, dann Fachmittelschule.) Ich kann dies nicht zweifelsfrei klarstellen, da ich mich dafür mit diesem “neuen” Ausbildungsmodell nicht ausreichend auskenne. Ich habe allerdings die Vorgängerausbildung zur Fachmittelschule, die dreijährige Diplommittelschule, besucht* und bin mir einiger Dinge, die sich seit Zeiten der Diplommittelschule nicht verändert haben, bewusst.
*DMS3-Diplom erlangt an einer Fachmittelschule – DMS angefangen und auch abgeschlossen, jedoch wurde der Ausbildungsgang während meiner Zeit dort umbenannt.